Question

已知抛物线y=-x²+bx+c的图象经过点A（m，0）、B（0，n），其中m、n是方程x²-6x+5=0的两个实数根，且m＜n．
（1）求抛物线的解析式；
（2）设（1）中的抛物线与x轴的另一个交点为C，抛物线的顶点为D，求C、D点的坐标和△BCD的面积；
（3）P是线段OC上一点，过点P作PH⊥x轴，交抛物线于点H，若直线BC把△PCH分成面积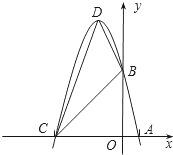相等的两部分，求P点的坐标．

Answer 1

解：（1）解方程x²-6x+5=0，
得x₁=5，x₂=1，
由m＜n，知m=1，n=5，
∴A（1，0），B（0，5），
∴
即；
所求抛物线的解析式为y=-x²-4x+5．

（2）由-x²-4x+5=0，
得x₁=-5，x₂=1，
故C的坐标为（-5，0），
由顶点坐标公式，得D（-2，9）；
过D作DE⊥x轴于E，易得E（-2，0），
∴S_△BCD=S_△CDE+S_梯形OBDE-S_△OBC=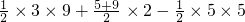=15．
（注：延长DB交x轴于F，由S_△BCD=S_△CFD-S_△CFB也可求得）

（3）设P（a，0），则H（a，-a²-4a+5）；
直线BC把△PCH分成面积相等的两部分，须且只须BC等分线段PH，亦即PH的中点，
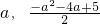（）在直线BC上，
易得直线BC方程为：y=x+5；
∴．
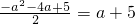解之得a₁=-1，a₂=-5（舍去），
故所求P点坐标为（-1，0）．
分析：（1）通过解方程可求出m、n的值，也就求出了点A、B的坐标，将它们代入抛物线的解析式中，通过联立方程组即可求得待定系数的值，从而确定该抛物线的解析式．
（2）抛物线的解析式中，令y=0可求得C点坐标，利用公式法可求出抛物线顶点D的坐标；由于△BCD的面积无法直接求得，可过D作x轴的垂线，设垂足为E，分别求出△CDE、梯形DEOB、△BCO的面积，那么△CDE、梯形DEOB的面积和减去△BCO的面积，即可得到△BCD的面积．
（3）若直线BC平分△PCH的面积，那么直线BC必过PH的中点，因为只有这样平分所得的两个三角形才等底等高，可设出点P的坐标，根据抛物线的解析式可表示出点H的坐标，进而可求得PH中点的坐标，由于PH中点在直线BC上，可将其代入直线BC的解析式中，由此求出点P的坐标．
点评：此题考查了一元二次方程的解法、二次函数解析式的确定、图形面积的求法、函数图象上点的坐标意义等基础知识，难度不大．