Question

（2013•南通一模）已知：如图，AB是⊙O的直径，C是⊙O上一点，OD⊥AC于点D，过点C作⊙O的切线，交OD的延长线与点E，连接AE．
（1）求证：AE与⊙O相切；
（2）连接BD并延长交AE于点F，若EC∥AB，OA=6，求AF的长．

Answer 1

分析：（1）连接OC，由CE为圆O的切线，利用切线的性质得到∠OCE=90°，再由OA=OC，OD垂直于AC，利用三线合一得到一对角相等，利用SAS得到三角形COE与三角形AOE全等，由全等三角形的对应角相等得到∠OAE=∠OCE=90°，利用垂直的定义得到AE与AO垂直，即可得证；
（2）设BF与OC交于点G，由EC与AB平行，利用两直线平行同旁内角互补，及三个角为直角的四边形为矩形得到四边形AECO为矩形，再由OA=OC，得到四边形AECO为正方形，可得出OG平行于AE，AE=AO=6，OD=ED，由OG与AF平行，利用平行线得比例得到OG=EF，再由OG与AF平行，得到比例式，得到AF=2OG=2EF，即可求出AF的长．

解答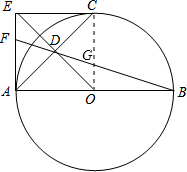：（1）证明：连接OC，
∵CE是⊙O的切线，
∴∠OCE=90°，
∵OA=OC，OD⊥AC，
∴∠COE=∠AOE，
∵在△COE和△AOE中，

OA=OC ∠COE=∠AOE OE=OE

，
∴△COE≌△AOE（SAS），
∴∠OAE=∠OCE=90°，
∴OA⊥AE，
∴AE与⊙O相切；

（2）解：设BF与OC相交于点G，
∵EC∥AB，
∴∠AEC=∠OAE=90°，
∵∠AEC=∠OAE=∠OCE=90°，
∴四边形OAEC是矩形，
∵OA=OC，
∴矩形OAEC是正方形，
∴OG∥AE，AE=AO=6，OD=ED，
∵OG∥AE，
∴

OG

EF

=

OD

ED

=1，
∴OG=EF，
∵OG∥AE，
∴

OG

AF

=

OB

AB

=

1

2

，
∴

EF

AF

=

1

2

，
∴AF=

2

3

AE=

2

3

×6=4．

点评：此题考查了切线的判定与性质，全等三角形的判定与性质，正方形的判定与性质，熟练掌握切线的判定与性质是解本题的关键．