Question

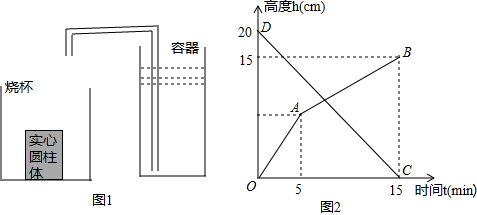
如图1，将一个放有一定量的水的圆柱型容器向一个放有实心小圆柱体的烧杯内注水，烧杯内及圆柱型容器内水面的高度h与注水时间t之间的函数图象如图2所示，已知烧杯的底面积为40cm²，实心小圆柱体底面积为10cm²，
（1）烧杯内水面的高度h₁与注水时间t之间的函数图象为

折线OAB

，圆柱型容器内水面的高度h₂与注水时间t之间的函数图象为

线段CD

 （填折线OAB或线段CD）
（2）求图中实心小圆柱体的高度和圆柱型容器的底面积．
（3）t为何值时，烧杯内及圆柱型容器内水面的高度相同？
（4）请直接写出t为何值时，烧杯内及圆柱型容器内水的质量相同？

Answer 1

分析：（1）由于是将圆柱型容器里面的水向烧杯内注水，所以烧杯内的水面逐渐上升，即水面的高度h₁随注水时间t的增大而增大，又因为烧杯底部放有一个实心小圆柱体，所以水面上升的高度先快后慢；圆柱型容器内的水面逐渐下降，即水面的高度h₂随注水时间t的增大而减小，由此得出烧杯内水面的高度h₁与注水时间t之间的函数图象为折线OAB，圆柱型容器内水面的高度h₂与注水时间t之间的函数图象为线段CD；
（2）设图中实心小圆柱体的高为xcm，由图2可知，当时间t=5min时，烧杯内水面的高度为xcm；所以当时间0＜t≤5min时，烧杯内的水面每分钟上升

x

5

cm，此时烧杯内装水的底面积为40-10=30cm²；当时间5＜t≤15min时，烧杯内的水面每分钟上升

15-x

15-5

cm，此时烧杯内装水的底面积为40cm²；由于匀速注水，所以水面上升的高度与底面积成反比，得出

x

5

：

15-x

15-5

=40：30，解方程求出x的值．再设圆柱型容器的底面积为ycm²，根据圆柱型容器内减少的水的体积=烧杯内增加的水的体积，列出关于y的方程，解方程即可；
（3）先利用待定系数法分别求出AB与CD的函数解析式，再令h₁=h₂，得到关于t的方程，解方程即可；
（4）由图2可知，15min可将圆柱型容器内的水全部注入烧杯，由于注水速度均匀，所以当t=

15

2

min时，圆柱型容器内的水有一半注入烧杯，即此时烧杯内及圆柱型容器内水的质量相同．

解答：解：（1）由题意可知，烧杯内水面的高度h₁与注水时间t之间的函数图象为折线OAB，圆柱型容器内水面的高度h₂与注水时间t之间的函数图象为线段CD；
故答案为：折线OAB，线段CD；

（2）设图中实心小圆柱体的高为xcm，由题意，得

x

5

：

15-x

15-5

=40：30，
解得x=6．
设圆柱型容器的底面积为ycm²，由题意，得
20y=30×6+40×（15-6），
解得y=27．
故图中实心小圆柱体的高度为6cm，圆柱型容器的底面积为27cm²；

（3）设AB的解析式为h₁=kt+b，
∵A（5，6），B（15，15）在此直线上，
∴

5k+b=6 15k+b=15

，
解得

k= 9 10 b= 3 2

，
∴AB的解析式为h₁=

9

10

t+

3

2

．
设CD的解析式为h₂=mt+n，
∵C（15，0），D（0，20）在此直线上，
∴

15m+n=0 n=20

，
解得

m=- 4 3 n=20

，
∴CD的解析式为h₂=-

4

3

t+20．
由h₁=h₂，得

9

10

t+

3

2

=-

4

3

t+20，
解得t=

555

67

．
故当t为

555

67

时，烧杯内及圆柱型容器内水面的高度相同；

（4）当t=

15

2

min时，烧杯内及圆柱型容器内水的质量相同．

点评：本题主要考查了一次函数的应用以及利用图象获取正确信息，识别函数图象的能力，观察图象提供的信息，再分析高度、时间和容积的关系即可找到解题关键．利用已知图象得出正确信息是考查重点．