Question

【题目】直线MN与x轴，y轴分别相交A、C两点，分别过A、C作x轴、y轴的垂线，二者相交于B点，且OA=8，OC=6.

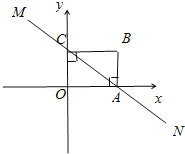
（1）求直线MN的解析式；

（2）已知在直线MN上存在点P，使△PBC是等腰三角形，求点P的坐标.

Answer 1

【答案】(1) y=- x+6；(2) P1（4，3）；P2（- ，），P3（，）；P4（，-）.

【解析】试题分析：（1）根据题意求出点A、C的坐标，运用待定系数法求出直线MN的解析式；

（2）从PC=PB，PC=BC，PB=BC三种情况进行解答．

试题解析：（1）∵OA=8，OC=6，

∴A（8，0），C（0，6），

设直线MN的解析式为：y=kx+b，

，解得：k＝ ，b＝6，

直线MN的解析式：y=- x+6；

（2）由题意得，B（8，6），

∵点P在直线MN上，

∴设P（a，-a+6），

当PC=PB时，点P为BC的中垂线与MN的交点，则P1（4，3）；

当PC=BC时，a2+（- a+6-6）2=64，

解得，a1= - ，a2= ，

则P2（- ，），P3（，）；

当PB=BC时，（a-8）2+（-a+6-6）2=64，

解得，a= ，

则P4（，-