题目内容
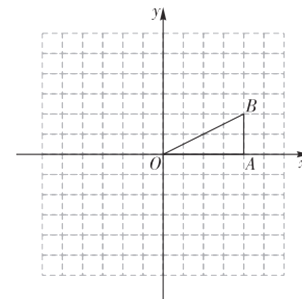
【题目】如图,直线y=kx+b与x轴、y轴分别交于点A,B,且OA,OB的长(OA > OB)是方程x2-10x +24=0的两个根,P(m,n)是第一象限内直线y=kx+b上的一个动点(点P不与点A,B重合).
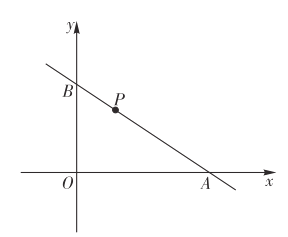
(1)求直线AB的解析式;
(2)C是x轴上一点,且OC=2,求△ACP的面积S与m之间的函数关系式;
(3)在x轴上是否存在点Q,使以A,B,Q为顶点的三角形是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ;(2)当C点在x正半轴时,
;(2)当C点在x正半轴时,![]() ;当C点在x负半轴时,
;当C点在x负半轴时,![]() ;(3)存在. Q1(6-
;(3)存在. Q1(6-![]() ,0),Q2(6+
,0),Q2(6+![]() ,0),Q3(-6,0),Q4(
,0),Q3(-6,0),Q4(![]() ,0).
,0).![]()
【解析】
(1)用待定系数法求直线表达式即可;(2)根据题意得出AC=4或8,根据面积公式计算;(3)根据等腰三角形的判断,分别以满足AQ=AB=![]() ,BQ=AB=
,BQ=AB=![]() ,QA=QB三种情况进行讨论计算,从而求Q点坐标.
,QA=QB三种情况进行讨论计算,从而求Q点坐标.
解:(1) ∵x2-10x+24=0,
(x -4)(x-6)=0,
∴x1 =4,x2 =6.
∵OA,OB的长是方程的两个根,且OA > OB,
∴OA =6,OB =4.
∴A(6,0),B(0,4).
把点A(6,0),B(0,4)代人y=kx +b中,![]() ,解得
,解得
∴直线AB的解析式为 ![]() .
.
(2) ∵直线AB的解析式为![]() ,点P(m,n)在直线AB上,
,点P(m,n)在直线AB上,
∴点P的纵坐标为![]() ,
,
当点C在x轴正半轴上时,0C=2,AC=4,
![]() =
= ![]() ;
;
当点C在x轴负半轴上时,OC=2,AC=8,
![]() =
= ![]() .
.
(3)存在.Q1(-6,0),Q2(6- 2![]() ,0),Q3
,0),Q3![]() ,Q4(6+2
,Q4(6+2![]() ,0).理由如下:
,0).理由如下:
∵A(6,0),B(0,4),∴AB=![]() .当△ABQ为等腰三角形,分三种情况:
.当△ABQ为等腰三角形,分三种情况:
①如图,当AQ=AB=![]() 时
时
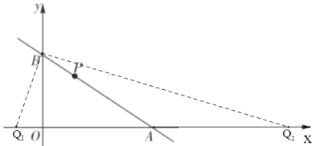
Q点坐标为Q1(6-![]() ,0)或Q2(6+
,0)或Q2(6+![]() ,0);
,0);
②如图,当BQ=BA=![]() 时
时
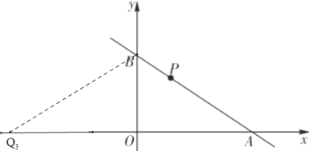
OA=OQ3=6,Q点坐标为Q3(-6,0);
③如图,当QA=QB时

设OQ4=t,则Q4A=Q4B=6-t,根据勾股定理得
42+t2=(6-t)2,
解得,t=![]()
∴Q点坐标为Q4(![]() ,0).
,0).
综上所述,符合题中条件的Q点有4个,坐标分别为Q1(6-![]() ,0),Q2(6+
,0),Q2(6+![]() ,0),Q3(-6,0),Q4(
,0),Q3(-6,0),Q4(![]() ,0).
,0).

 阅读快车系列答案
阅读快车系列答案【题目】二次函数![]() (
(![]() 是常数,
是常数,![]() )的自变量
)的自变量![]() 与函数值
与函数值![]() 的部分对应值如下表:
的部分对应值如下表:
| … |
|
| 0 | 1 | 2 | … |
| … |
|
|
|
|
| … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②
;②![]() 和3是关于
和3是关于![]() 的方程
的方程![]() 的两个根;③
的两个根;③![]()
![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
【题目】小明和小李准备七月初到重庆或长沙去旅游,为了了解这两个城市哪个更热,他们查阅资料,收集了两个城市2018年七月前两周最高温度的记录,如下表:
日期(七月) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
重庆最高温度/℃ | 33 | 36 | 34 | 31 | 31 | 30 | 30 | 33 | 34 | 36 | 37 | 35 | 37 | 37 |
长沙最高温度/℃ | 29 | 34 | 35 | 35 | 36 | 29 | 31 | 31 | 34 | 35 | 35 | 31 | 35 | 35 |
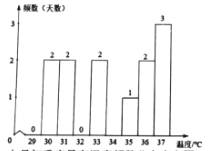
根据上表,他们将两个城市的最高温度分别绘制了如下的频数分布直方图和统计表,并对数据进行了整理
七月初重庆最高温度频数分布直方图
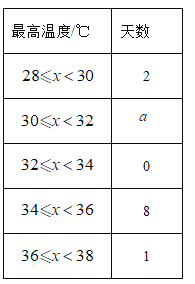
七月初长沙最高温度统计表
平均数/℃ | 中位数/℃ | 众数/℃ | 34/℃以上天数 | 30/℃以下天数 | |
重庆 | 33.9 | 34 | c | 6 | 0 |
长沙 | 33.2 | b | 35 | 7 | 2 |
请回答如下问题:
(1)本次调查的目的是________;
(2)补全频数分布直方图,并写出表中a,b,c的值,![]() ________,
________,![]() _____,c=___.
_____,c=___.
(3)结合以上分析,你认为七月初哪个城市更热,请写出两条支持你观点的理由.