题目内容
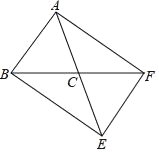
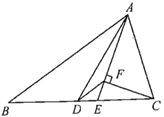
【题目】如图所示,在![]() 中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=
中,AB>AC,AD是中线,AE是角平分线,CF⊥AE于点F,连接DF,则①DF//AB;②∠DAE=![]() (∠ACB-∠ABC);③DF=
(∠ACB-∠ABC);③DF=![]() (AB-AC);④
(AB-AC);④![]() (AB-AC)<AD<
(AB-AC)<AD<![]() (AB+AC).其中正确的是__________.
(AB+AC).其中正确的是__________.
【答案】①③④
【解析】
延长CF交AB于点H,证明F是CH的中点,再根据中位线的性质即可判断①和③;延长AD到M使得AD=DM,证明△ADC≌△MDB可得BM=AC,再利用三角形的三边关系即可判断④.
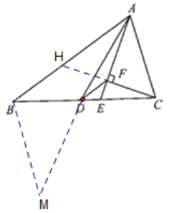
延长CF交AB于点H
∵AE是∠BAC的角平分线,CF⊥AE
∴△ACH是等腰三角形,F是CH的中点
又AD是△ABC的中线
∴点D是BC的中点
∴DF∥AB,故①正确;
无法得出∠DAE=![]() (∠ACB-∠ABC),故②错误;
(∠ACB-∠ABC),故②错误;
∵DF是△CBG的中位线
∴DF=![]() BG=
BG=![]() (AB-AG)=
(AB-AG)=![]() (AB-AC),故③正确;
(AB-AC),故③正确;
延长AD到M使得AD=DM
在△ADC和△MDB中
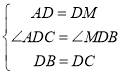
∴△ADC≌△MDB
∴BM=AC
∵AB-BM<AM<AB+BM
∴AB-AC<AM<AB+AC
∴![]() (AB-AC)<AD<
(AB-AC)<AD<![]() (AB+AC),故④正确;
(AB+AC),故④正确;
故答案选择①③④.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目