题目内容
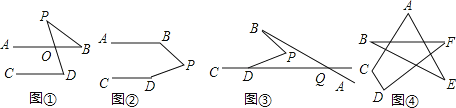
【题目】如图①,若AB∥CD,点P在AB,CD外部,则有∠D=∠BOD,又因为∠BOD是△POB的外角,故∠BOD=∠BPD+∠B,得∠BPD=∠D﹣∠B.
探究一:将点P移到AB,CD内部,如图②,则∠BPD,∠B,∠D之间有何数量关系?并证明你的结论;
探究二:在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD延长线于点Q,如图③,则∠BPD,∠B,∠PDQ,∠BQD之间又有何数量关系?并证明你的结论;
探究三:在图④中,直接根据探究二的结论,写出∠A+∠B+∠C+∠D+∠E+∠F的度数.
【答案】探究一:∠B+∠BPD+∠D=360°;探究二:∠BPD=∠B+∠PDQ+∠BQD;探究三:360°.
【解析】
试题分析:探究一,过点P作PE∥AB,根据平行线的性质可知∠B+∠BPE=180°,∠D+∠EPD=180°,即∠B+∠BPD+∠D=360°.
探究二,连接QP并延长至E,根据∠BPE是△BPQ的一个外角,得到∠BPE=∠BQP+∠B.同理得到∠EPD=∠DQP+∠PDQ,从而∠BPD=∠B+∠PDQ+∠BQD.
探究三,根据三角形外角性质和四边形的内角和等于360°得出即可.
探究一,∠B+∠BPD+∠D=360°,
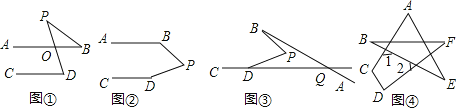
证明:过点P作PE∥AB,如图②,
∴∠B+∠BPE=180°,
又∵AB∥CD,
∴PE∥CD,
∴∠D+∠EPD=180°,
∴∠B+∠BPE+∠D+∠EPD=360°,
即∠B+∠BPD+∠D=360°;
探究二,∠BPD=∠B+∠PDQ+∠BQD,
证明:连接QP并延长至E,如图③,
∵∠BPE是△BPQ的一个外角,
∴∠BPE=∠BQP+∠B.
同理:∠EPD=∠DQP+∠PDQ.
∴∠BPE+∠EPD=∠BQP+∠B+∠DQP+∠PDQ.
即:∠BPD=∠B+∠PDQ+∠BQD;
探究三,如图④,∵∠1=∠A+∠E,∠2=∠B+∠F,∠1+∠2+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.