题目内容
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC. 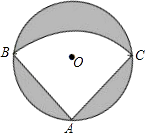
(1)求被剪掉阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
【答案】
(1)解:如图,连接BC,

∵∠BAC=90°,
∴BC为⊙O的直径,即BC=1m,
又∵AB=AC,
∴AB= ![]() BC=
BC= ![]() .
.
∴S阴影部分=S⊙O﹣S扇形ABC=π×( ![]() )2﹣
)2﹣ ![]() =
= ![]() (平方米)
(平方米)
(2)解:设底面圆的半径为r,则 ![]() π=2πr,
π=2πr,
∴r= ![]() m
m
圆锥的底面圆的半径长为 ![]() 米
米
【解析】(1)由∠BAC=90°,得BC为⊙O的直径,即BC=1m;又由AB=AC,得到AB= ![]() BC=
BC= ![]() ,而S阴影部分=S⊙O﹣S扇形ABC , 然后根据扇形和圆的面积公式进行计算即可;(2)扇形的半径是2sin45°=
,而S阴影部分=S⊙O﹣S扇形ABC , 然后根据扇形和圆的面积公式进行计算即可;(2)扇形的半径是2sin45°= ![]() ,扇形的弧长l=
,扇形的弧长l= ![]() =
= ![]() ,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
,圆锥的底面周长等于侧面展开图的扇形弧长,然后利用弧长公式计算.
【考点精析】本题主要考查了扇形面积计算公式和圆锥的相关计算的相关知识点,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.才能正确解答此题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目