题目内容
已知二次函数图象的顶点坐标为M(2,0),直线y=x+2与该二次函数的图象交于A、B两点,其中点A在y轴上(如图示)(1)求该二次函数的解析式;
(2)P为线段AB上一动点(A、B两端点除外),过P作x轴的垂线与二次函数的图象交于点Q,设线段PQ的长为l,点P的横坐标为x,求出l与x之间的函数关系式,并求出自变量x的取值范围;
(3)在(2)的条件下,线段AB上是否存在一点P,使四边形PQMA为梯形?若存在
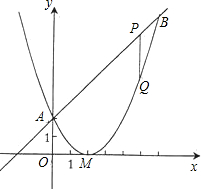 ,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
分析:(1)先根据直线的解析式求出A点的坐标,然后根据M点的坐标,用顶点式二次函数通式来设抛物线的解析式,将A点的坐标代入抛物线中即可求出二次函数的解析式.
(2)PQ的长,实际是直线AB的函数值与抛物线的函数值的差.据此可得出l,x的函数关系式.
(3)要想使PQMA为梯形,只有一种情况,即MQ∥AP,可根据直线AB的斜率和M点的坐标求出直线MQ的解析式,联立抛物线的解析式即可求出Q点的坐标,将Q的横坐标代入直线AB中即可求出P点的坐标,得出然后可根据A,M,Q,P的坐标求出AP,MQ,AM的长,进而可求出梯形AMQP的面积(可设直线AB与x轴的交点为N,利用∠ANO=45°来求个各边的长).
(2)PQ的长,实际是直线AB的函数值与抛物线的函数值的差.据此可得出l,x的函数关系式.
(3)要想使PQMA为梯形,只有一种情况,即MQ∥AP,可根据直线AB的斜率和M点的坐标求出直线MQ的解析式,联立抛物线的解析式即可求出Q点的坐标,将Q的横坐标代入直线AB中即可求出P点的坐标,得出然后可根据A,M,Q,P的坐标求出AP,MQ,AM的长,进而可求出梯形AMQP的面积(可设直线AB与x轴的交点为N,利用∠ANO=45°来求个各边的长).
解答:解:(1)依题意,设二次函数的解析式为y=a(x-2)2,
由于直线y=x+2与y轴交于(0,2),
∴x=0,y=2
满足y=a(x-2)2,于是求得a=
,
二次函数的解析式为y=
(x-2)2;
(2)设P点坐标为:P(x,y),则Q点坐标为(x,
x2-2x+2)
依题意得,PQ=l=(x+2)-
(x-2)2=-
x2+3x,
由
,
求得点B的坐标为(6,8),
∴0<x<6;
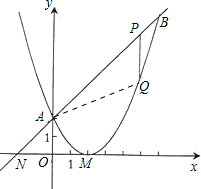
(3)由(2)知P的横坐标为0<x<6时,必有对应的点Q在抛物线上;
反之,Q的横坐标为0<x<6时,在线段AB上必有一点P与之对应.
假设存在符合条件的点P,由题意得AM与PQ不会平行,
因此梯形的两底只能是AP与MQ,
∵过点M(2,0)且平行AB的直线方程为y=x-2,
由
,
消去y得:x2-6x+8=0,即(x-2)(x-4)=0,
解得x=2或x=4,
∵当x=2时,P点、Q点、M点 三点共线,与A点只能构成三角形,而不能构成梯形;
∴x=2这个解舍去.
∴过M点的直线与抛物线的另一交点为(4,2),
∵此交点横坐标4,落在0<x<6范围内,
∴Q的坐标为(4,2)时,P(4,6)符合条件,
即存在符合条件的点P,其坐标为(4,6),
设直线AB与x轴交于N,由条件可知,△ANM是等腰直角三角形,即AM=AN=2
,
AP=PN-AN=6
-2
=4
,MQ=2
,
AM为梯形PQMA的高,
故S梯形PQMA=
(2
+4
)•2
=12.
由于直线y=x+2与y轴交于(0,2),
∴x=0,y=2
满足y=a(x-2)2,于是求得a=
| 1 |
| 2 |
二次函数的解析式为y=
| 1 |
| 2 |
(2)设P点坐标为:P(x,y),则Q点坐标为(x,
| 1 |
| 2 |
依题意得,PQ=l=(x+2)-
| 1 |
| 2 |
| 1 |
| 2 |
由
|
求得点B的坐标为(6,8),
∴0<x<6;

(3)由(2)知P的横坐标为0<x<6时,必有对应的点Q在抛物线上;
反之,Q的横坐标为0<x<6时,在线段AB上必有一点P与之对应.
假设存在符合条件的点P,由题意得AM与PQ不会平行,
因此梯形的两底只能是AP与MQ,
∵过点M(2,0)且平行AB的直线方程为y=x-2,
由
|
消去y得:x2-6x+8=0,即(x-2)(x-4)=0,
解得x=2或x=4,
∵当x=2时,P点、Q点、M点 三点共线,与A点只能构成三角形,而不能构成梯形;
∴x=2这个解舍去.
∴过M点的直线与抛物线的另一交点为(4,2),
∵此交点横坐标4,落在0<x<6范围内,
∴Q的坐标为(4,2)时,P(4,6)符合条件,
即存在符合条件的点P,其坐标为(4,6),
设直线AB与x轴交于N,由条件可知,△ANM是等腰直角三角形,即AM=AN=2
| 2 |
AP=PN-AN=6
| 2 |
| 2 |
| 2 |
| 2 |
AM为梯形PQMA的高,
故S梯形PQMA=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了二次函数解析式的确定、图形的面积求法、函数图象交点、梯形的判定等知识及综合应用知识、解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 OC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
OC相似?若存在,请求出P点的坐标;若不存在,请说明理由. 已知二次函数图象的顶点是(-1,2),且过点
已知二次函数图象的顶点是(-1,2),且过点 已知二次函数图象的顶点坐标为M(3,-2),且与y轴交于N(0,
已知二次函数图象的顶点坐标为M(3,-2),且与y轴交于N(0, 点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
点(A在B的左侧),且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点. 于点Q,设线段PQ的长为l,点P的横坐标为x.
于点Q,设线段PQ的长为l,点P的横坐标为x.