题目内容
某公司为了扩大经营,决定购进6台机器用于生产某种活塞,现有甲、乙两种机器选择,其中每种机器的价格和每台机器生产活塞的数量如下表:| 甲 | 乙 | |
| 价格(万元/1台) | 7 | 5 |
| 每台日产量(个) | 100 | 60 |
(1)设甲种机器购买x台,本次购买机器所耗资为y万元,试求出y与x之间的函数关系式,并帮助公司确定有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于500个,那么为了节约资金应选择哪种购买方案?
分析:(1)根据题意可知y=2x+30,利用“甲种机器购买的台数不能少于总台数的一半”“购买机器所耗资金不能超过40万元”可得到3≤x≤5,因为x为整数,∴x=3,4,5,故有三种购买方案;
(2)根据“日生产能力不能低于500个”可得100x+60(6-x)≥500,即得到x=4或5,y随x的增大而增大,考虑节约资金,应取x=4时的方案.
(2)根据“日生产能力不能低于500个”可得100x+60(6-x)≥500,即得到x=4或5,y随x的增大而增大,考虑节约资金,应取x=4时的方案.
解答:解:(1)y与x之间的函数关系式为:y=7x+5(6-x)=2x+30,
∵
?3≤x≤5,
∵x为整数,
∴x=3,4,5,故有三种购买方案;
(2)由100x+60(6-x)≥500,
解得:x≥
,
∴x=4,5
∵k=2>0,
∴y随x的增大而增大,
∴考虑节约资金,应取x=4时的方案.
∵
|
∵x为整数,
∴x=3,4,5,故有三种购买方案;
(2)由100x+60(6-x)≥500,
解得:x≥
| 7 |
| 2 |
∴x=4,5
∵k=2>0,
∴y随x的增大而增大,
∴考虑节约资金,应取x=4时的方案.
点评:主要考查利用一次函数的模型解决实际问题的能力.要先根据题意列出函数关系式,再代数求值.解题的关键是要分析题意根据实际意义求解.注意要根据实际意义准确的找到不等关系,利用不等式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
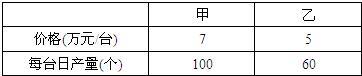 16、某公司为了扩大经营,决定购进6台机器用于生产某种机器零件.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产机器零件的数量如下表所示.经过预算,本次购买机器所用资金不能超过34万元.按该公司要求可以有几种购买方案?
16、某公司为了扩大经营,决定购进6台机器用于生产某种机器零件.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产机器零件的数量如下表所示.经过预算,本次购买机器所用资金不能超过34万元.按该公司要求可以有几种购买方案?