题目内容
某公司为了扩大经营,决定购进6台机器用于生产某种活塞.现有甲、乙两种型号机器供选择,其中每种型号机器的价格如下表所示.经过预算,本次购买机器所耗资金不能超过68万元.
(1)若设购买甲种型号机器x台,则购买乙种型号机器为
(2)求该公司共有哪几种购买机器的方案?
| 机器型号 | 甲 | 乙 |
| 价格(万元/台) | 14 | 10 |
(6-x)
(6-x)
台(用含x的代数式表示);(2)求该公司共有哪几种购买机器的方案?
分析:(1)根据甲乙两种型号的机器共6台,就可以表示出乙种型号的机器=(6-x)得出结论;
(2)根据甲种型号的机器的价格+乙种型号的机器的价格≤68万元建立不等式求出其解就可以得出结论.
(2)根据甲种型号的机器的价格+乙种型号的机器的价格≤68万元建立不等式求出其解就可以得出结论.
解答:解:(1)由题意,得
购买乙种型号机器为:(6-x)台,
(2)依题意得:
14x+10(6-x)≤68,
解得:x≤2,
又x≥0且x为整数,∴x=0,或x=1或x=2,
所以,该公司共有三种购买方案如下:
方案一:甲种机器0台,则购买乙种机器6台;
方案二:甲种机器1台,则购买乙种机器5台;
方案三:甲种机器2台,则购买乙种机器4台.
故答案为:(6-x).
购买乙种型号机器为:(6-x)台,
(2)依题意得:
14x+10(6-x)≤68,
解得:x≤2,
又x≥0且x为整数,∴x=0,或x=1或x=2,
所以,该公司共有三种购买方案如下:
方案一:甲种机器0台,则购买乙种机器6台;
方案二:甲种机器1台,则购买乙种机器5台;
方案三:甲种机器2台,则购买乙种机器4台.
故答案为:(6-x).
点评:本题考查了代数式表示数的运用,列一元一次不等式解实际问题的运用,方案设计题型的运用,解答时根据条件建立不等式求出其解是关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
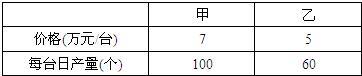 16、某公司为了扩大经营,决定购进6台机器用于生产某种机器零件.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产机器零件的数量如下表所示.经过预算,本次购买机器所用资金不能超过34万元.按该公司要求可以有几种购买方案?
16、某公司为了扩大经营,决定购进6台机器用于生产某种机器零件.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产机器零件的数量如下表所示.经过预算,本次购买机器所用资金不能超过34万元.按该公司要求可以有几种购买方案?