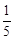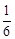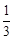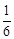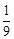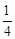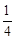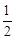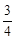题目内容
某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同打乱顺序重新排列,从中任意抽取1张卡片
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.
(1)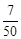 (2)不公平(3)见解析
(2)不公平(3)见解析
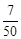 (2)不公平(3)见解析
(2)不公平(3)见解析解:(1)∵在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),
∴是20倍数或者能整除20的数有7个。
∴取到的卡片上序号是20的倍数或能整除20的概率为: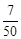 。
。
(2)不公平。理由如下:
∵无论k取何值,都能被1整除,则序号为1的学生被抽中的概率为1,即100%,
而很明显抽到其他序号学生概率不为100%,如序号为2的学生被抽中的概率为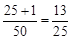 ,
,
∴这一规定不公平。
(3)如:设序号1~10的10名学生为A组,序号11~20的10名学生为B组,序号21~300的10名学生为C组,序号31~40的10名学生为D组,序号41~50的10名学生为E组,随机抽取一组,则因为每个学生被抽取的概率都是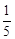 ,所以符合要求。
,所以符合要求。
又如:先抽出一张,记下数字,然后放回.若下一次抽到的数字与之前抽到过的重复,则不记数,放回,重新抽取.不断重复,直至抽满10个不同的数字为止,,则因为每个学生被抽取的概率都是 ,所以符合要求。
,所以符合要求。
(1)由在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),直接利用概率公式求解即可求得答案。
(2)游戏公平性就是要每个事件的概率相等,概率相等就公平,否则就不公平。因此,由无论k取何值,都能被1整除,则序号为1的学生被抽中的概率为1,即100%,而很明显抽到其他序号学生概率不为100%.可知此游戏不公平。
(3)设计一个规则,使每个事件的概率相等即可。答案不唯一。
∴是20倍数或者能整除20的数有7个。
∴取到的卡片上序号是20的倍数或能整除20的概率为:
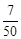 。
。(2)不公平。理由如下:
∵无论k取何值,都能被1整除,则序号为1的学生被抽中的概率为1,即100%,
而很明显抽到其他序号学生概率不为100%,如序号为2的学生被抽中的概率为
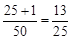 ,
,∴这一规定不公平。
(3)如:设序号1~10的10名学生为A组,序号11~20的10名学生为B组,序号21~300的10名学生为C组,序号31~40的10名学生为D组,序号41~50的10名学生为E组,随机抽取一组,则因为每个学生被抽取的概率都是
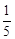 ,所以符合要求。
,所以符合要求。又如:先抽出一张,记下数字,然后放回.若下一次抽到的数字与之前抽到过的重复,则不记数,放回,重新抽取.不断重复,直至抽满10个不同的数字为止,,则因为每个学生被抽取的概率都是
 ,所以符合要求。
,所以符合要求。(1)由在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),直接利用概率公式求解即可求得答案。
(2)游戏公平性就是要每个事件的概率相等,概率相等就公平,否则就不公平。因此,由无论k取何值,都能被1整除,则序号为1的学生被抽中的概率为1,即100%,而很明显抽到其他序号学生概率不为100%.可知此游戏不公平。
(3)设计一个规则,使每个事件的概率相等即可。答案不唯一。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目