题目内容
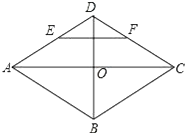
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 与边
与边![]() 分别交于
分别交于![]() 两点,过点
两点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.

⑴求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
⑵若![]() ,求
,求![]() 的长
的长
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)证明:如图,连接OD,作OG⊥AC于点G,推出∠ODB=∠C;然后根据DF⊥AC,∠DFC=90°,推出∠ODF=∠DFC=90°,即可推出DF是⊙O的切线.(2)首先判断出:AG=![]() AE=2,然后判断出四边形OGFD为矩形,即可求出DF的值.
AE=2,然后判断出四边形OGFD为矩形,即可求出DF的值.
试题解析:
(1)证明:如图,连接OD,作OG⊥AC于点G,

∵OB=OD,
∴∠ODB=∠B,
又∵AB=AC,
∴∠C=∠B,
∴∠ODB=∠C,
∵DF⊥AC,
∴∠DFC=90°,
∴∠ODF=∠DFC=90°,
∴DF是⊙O的切线.
(2)解:AG=![]() AE=2,
AE=2,
∵cosA=![]() ,
,
∴OA=![]() =
=![]() =5,
=5,
∴OG=![]() ,
,
∵∠ODF=∠DFG=∠OGF=90°,
∴四边形OGFD为矩形,
∴DF=OG=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目