题目内容
若a,b,c互不相等,则方程(a2+b+c2)x2+2(a+b+c)x+3=0
- A.有两个相等的实数根
- B.有两个不相等的实数根
- C.没有实数根
- D.根的情况不确定
C
因为Δ=4(a+b+c)2-12(a2+b2+c2)
=4(-2a2-2b2-2c2+2ab+2ac+2bc)
=-4[(a-b)2+(b-c)2+(c-a)2]<0
因为Δ=4(a+b+c)2-12(a2+b2+c2)
=4(-2a2-2b2-2c2+2ab+2ac+2bc)
=-4[(a-b)2+(b-c)2+(c-a)2]<0

练习册系列答案
相关题目
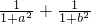 的值为
的值为
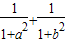 的值为( )
的值为( )