题目内容
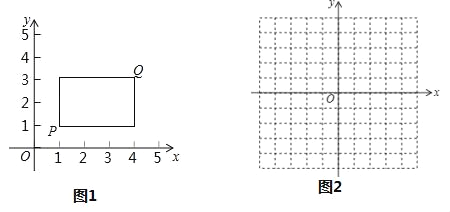
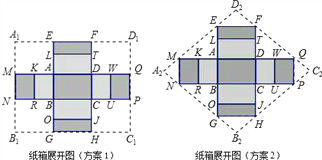
【题目】葡萄在销售时,要求“葡萄”用双层上盖的长方体纸箱封装(上盖纸板面积刚好等于底面面积的2倍),如图
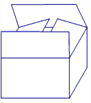
(1)实际运用:如果要求纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比, 取黄金比为0.6),体积为0.3立方米.
①按方案1(如图)做一个纸箱,需要矩形硬纸板A1B1C1D1的面积是多少平方米?
②小明认为,如果从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2 做一个纸箱比方案1更优,你认为呢?请说明理由.
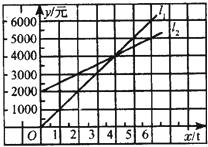
(2)拓展思维:水果商打算在产地购进一批“葡萄”,但他感觉(1)中的纸箱体积太大,搬运吃力,要求将纸箱的底面周长、底面面积和高都设计为原来的一半,你认为水果商的要求能办到吗?请利用函数图象验证.

【答案】解:(1)①∵纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比,取黄金比为0.6),体积为0.3立方米,
∴假设底面长为x,宽就为0.6x,
∴体积为:0.6xx0.5=0.3,
解得:x=1,
∴AD=1,CD=0.6,
DW=KA=DT=JC=0.5,FT=JH=![]() CD=0.3,
CD=0.3,
WQ=MK=![]() AD=
AD=![]() ,
,
∴QM=![]() +0.5+1+0.5+
+0.5+1+0.5+![]() =3,
=3,
FH=0.3+0.5+0.6+0.5+0.3=2.2,
∴矩形硬纸板A1B1C1D1的面积是3×2.2=6.6平方米;
②从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
∵如图可知△MAE,△NBG,△HCF,△FDQ面积相等,且和为2个矩形FDQD1,
又∵菱形的性质得出,对角线乘积的一半绝对小于矩形边长乘积;
∴从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
(2)∵将纸箱的底面周长、底面面积和高都设计为原来的一半时,
∴边长为:0.5,0.3,底面积将变为:0.3×0.5=0.15,将变为原来的![]() ,高再变为原来的一半时,体积将变为原来的
,高再变为原来的一半时,体积将变为原来的![]() ,
,
∴水果商的要求不能办到.
【解析】试题分析:(1)①利用宽与长的比是黄金比,取黄金比为0.6,假设底面长为x,宽就为0.6x,再利用图形得出QM=0.5+0.5+1+0.5+0.5=3,FH=0.3+0.5+0.6+0.5+0.3=2.2,进而求出即可;
②根据菱形的性质得出,对角线乘积的一半绝对小于矩形边长乘积即可得出答案;
(2)根据相似三角形的性质面积比等于相似比的平方得出即可.
试题解析:
解:(1)①∵纸箱的高为0.5米,底面是黄金矩形(宽与长的比是黄金比,取黄金比为0.6),体积为0.3立方米,
∴假设底面长为x,宽就为0.6x,
∴体积为:0.6xx0.5=0.3,解得:x=1,
∴AD=1,CD=0.6,DW=KA=DT=JC=0.5,FT=JH=![]() CD=0.3,
CD=0.3,
WQ=MK=![]() AD=
AD=![]() ,
,
∴QM=![]() +0.5+1+0.5+
+0.5+1+0.5+![]() =3,
=3,
FH=0.3+0.5+0.6+0.5+0.3=2.2,
∴矩形硬纸板A1B1C1D1的面积是3×2.2=6.6平方米;
②从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
∵如图可知△MAE,△NBG,△HCF,△FDQ面积相等,且和为2个矩形FDQD1,
又∵菱形的性质得出,对角线乘积的一半绝对小于矩形边长乘积;
∴从节省材料的角度考虑,采用方案2(如图)的菱形硬纸板A2B2C2D2做一个纸箱比方案1更优,
(2)∵将纸箱的底面周长、底面面积和高都设计为原来的一半时,
∴边长为:0.5,0.3,底面积将变为:0.3×0.5=0.15,将变为原来的![]() ,高再变为原来的一半时,体积将变为原来的
,高再变为原来的一半时,体积将变为原来的![]() ,
,
∴水果商的要求不能办到.

【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称 | 空调 | 彩电 | 冰箱 |
工 时 |
|
|
|
产值(千元) | 4 | 3 | 2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高最高产值是多少?(以千元为单位)
【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时) | 挖掘土石方量(单位:m3/台时) | |
甲型挖掘机 | 100 | 60 |
乙型挖掘机 | 120 | 80 |
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?