题目内容
(2012•工业园区一模)在△ABC中,AB=AC=5,∠A是锐角,sinA=
,
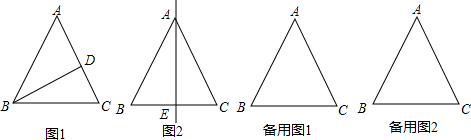
(1)如图1,作BD⊥AC垂足为D,求BD、BC的长:
(2)如图2,小明同学过点A作AE⊥BC垂足为E,他发现直线AE平分△ABC的周长和面积,他想是否还存在其它平分△ABC的周长和面积的直线?请你参与小明的探究,如果存在,请说明理由,同时指出有几条直线.(注:备用图不够用可以重新画图)
| 24 | 25 |
(1)如图1,作BD⊥AC垂足为D,求BD、BC的长:
(2)如图2,小明同学过点A作AE⊥BC垂足为E,他发现直线AE平分△ABC的周长和面积,他想是否还存在其它平分△ABC的周长和面积的直线?请你参与小明的探究,如果存在,请说明理由,同时指出有几条直线.(注:备用图不够用可以重新画图)

分析:(1)由BD垂直于AC,得到三角形ABD为直角三角形,根据AB及sinA的值,利用锐角三角函数定义求出BD及AD的长,再由AC-AD求出DC的长,在直角三角形BDC中,利用勾股定理即可求出BC的长;
(2)还存在2条其它平分△ABC的周长和面积的直线,理由为:若直线经过B(或C)点,由直线平分△ABC的面积,则直线必经过AC(或AB)的中点,而此时直线必不平分△ABC的周长,故直线不经过△ABC的顶点,分两种情况考虑:(i)直线与AB(或AC)、BC相交,设直线与AB、BC相交于点D、E,过A、D分别作BC的垂线,垂足为F、H点,如备用图1所示,假设DE平分三角形的周长,设BD=5k,则DF=4k,BE=8-5k,利用三角形的面积公式表示出BDF的面积,根据此三角形面积为三角形ABC面积的一半列出关于k的方程,求出方程的解得到k的值,可得出在BC上取BE=5,在BA上取BD=3,过D、E的直线就是所求的,同理AC,BC相交的直线也存在一条;(ii)直线与AB,AC相交,设直线与AB,AC分别交于D,E,过D作DF⊥AC,垂足为F点,如备用图2所示,设AE=x,则AD=8-x,根据三角形ADE的面积为三角形ABC面积的一半列出关于x的方程,求出方程的解得到x的值,经判断不合题意,舍去,综上,得到满足题意的直线有2条.
(2)还存在2条其它平分△ABC的周长和面积的直线,理由为:若直线经过B(或C)点,由直线平分△ABC的面积,则直线必经过AC(或AB)的中点,而此时直线必不平分△ABC的周长,故直线不经过△ABC的顶点,分两种情况考虑:(i)直线与AB(或AC)、BC相交,设直线与AB、BC相交于点D、E,过A、D分别作BC的垂线,垂足为F、H点,如备用图1所示,假设DE平分三角形的周长,设BD=5k,则DF=4k,BE=8-5k,利用三角形的面积公式表示出BDF的面积,根据此三角形面积为三角形ABC面积的一半列出关于k的方程,求出方程的解得到k的值,可得出在BC上取BE=5,在BA上取BD=3,过D、E的直线就是所求的,同理AC,BC相交的直线也存在一条;(ii)直线与AB,AC相交,设直线与AB,AC分别交于D,E,过D作DF⊥AC,垂足为F点,如备用图2所示,设AE=x,则AD=8-x,根据三角形ADE的面积为三角形ABC面积的一半列出关于x的方程,求出方程的解得到x的值,经判断不合题意,舍去,综上,得到满足题意的直线有2条.
解答:解:(1)∵BD⊥AC,
∴∠ADB=90°,
∵在Rt△ABD中,AB=AC=5,sinA=
,
∴BD=ABsinA=5×
=
,
∴根据勾股定理得:AD=
=
,
∴DC=AC-AD=5-
=
,
在Rt△BCD中,根据勾股定理得:BC=
=6;
(2)还存在2条其它平分△ABC的周长和面积的直线,理由为:
若直线经过B(或C)点,由直线平分△ABC的面积,则直线必经过AC(或AB)的中点,
而此时直线必不平分△ABC的周长,故直线不经过△ABC的顶点,
分两种情况考虑:
(i)直线与AB(或AC)、BC相交,设直线与AB、BC相交于点D、E,过A、D分别作BC的垂线,垂足为F、H点,
如备用图1所示:
∵AB=AC=5,AH⊥BC,
∴BH=CH=
BC=3,
在Rt△ABH中,根据勾股定理得:AH=
=4,
∴∠DFB=∠AHB=90°,又∠B=∠B,
∴△BDF∽△BAH,
∴BF:FD:BD=BH:AH:AB=3:4:5,
又∵三角形ABC的周长为5+5+6=16,
∴BD+BE=8,
设BD=5k,则DF=4k,BE=8-5k,
∴S△BDE=
S△ABC=
BC•AH=6,即
BE•DF=
=6,
整理得:5k2-8k+3=0,
解得:k=
或k=1(舍去),
这时在BC上取BE=5,在BA上取BD=3,过D、E的直线就是所求的,
同理AC,BC相交的直线也存在一条;
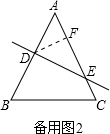
(ii)直线与AB,AC相交,设直线与AB,AC分别交于D,E,过D作DF⊥AC,垂足为F点,
如备用图2所示:
设AE=x,则AD=8-x,
∵在Rt△ADF中,sinA=
,
∴DF=ADsinA=
(8-x),
当S△AED=
AE•DF=
•x•
(8-x)=6,
整理得:2x2-16x+25=0,
解得:x1=4+
>5(舍去),x2=4-
,
则AD=8-x=4+
>5(不合题意,舍去),
综上,还存在2条其它平分△ABC的周长和面积的直线.
∴∠ADB=90°,
∵在Rt△ABD中,AB=AC=5,sinA=
| 24 |
| 25 |
∴BD=ABsinA=5×
| 24 |
| 25 |
| 24 |
| 5 |
∴根据勾股定理得:AD=
25-(
|
| 7 |
| 5 |
∴DC=AC-AD=5-
| 7 |
| 5 |
| 18 |
| 5 |
在Rt△BCD中,根据勾股定理得:BC=
(
|
(2)还存在2条其它平分△ABC的周长和面积的直线,理由为:
若直线经过B(或C)点,由直线平分△ABC的面积,则直线必经过AC(或AB)的中点,
而此时直线必不平分△ABC的周长,故直线不经过△ABC的顶点,
分两种情况考虑:
(i)直线与AB(或AC)、BC相交,设直线与AB、BC相交于点D、E,过A、D分别作BC的垂线,垂足为F、H点,
如备用图1所示:

∵AB=AC=5,AH⊥BC,
∴BH=CH=
| 1 |
| 2 |
在Rt△ABH中,根据勾股定理得:AH=
| AB2-BH2 |
∴∠DFB=∠AHB=90°,又∠B=∠B,
∴△BDF∽△BAH,
∴BF:FD:BD=BH:AH:AB=3:4:5,
又∵三角形ABC的周长为5+5+6=16,
∴BD+BE=8,
设BD=5k,则DF=4k,BE=8-5k,
∴S△BDE=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 4k(8-5k) |
| 2 |
整理得:5k2-8k+3=0,
解得:k=
| 3 |
| 5 |
这时在BC上取BE=5,在BA上取BD=3,过D、E的直线就是所求的,
同理AC,BC相交的直线也存在一条;
(ii)直线与AB,AC相交,设直线与AB,AC分别交于D,E,过D作DF⊥AC,垂足为F点,
如备用图2所示:
设AE=x,则AD=8-x,
∵在Rt△ADF中,sinA=
| 24 |
| 25 |

∴DF=ADsinA=
| 24 |
| 25 |
当S△AED=
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 25 |
整理得:2x2-16x+25=0,
解得:x1=4+
| ||
| 2 |
| ||
| 2 |
则AD=8-x=4+
| ||
| 2 |
综上,还存在2条其它平分△ABC的周长和面积的直线.
点评:此题考查了相似性综合题,涉及的知识有:勾股定理,锐角三角函数定义,一元二次方程的应用,以及解直角三角形,利用了数形结合及分类讨论的思想,是一道多知识的探究题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
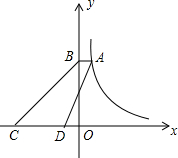 (2012•工业园区一模)如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D为x轴上动点,若CD=3AB,四边形ABCD的面积为4,则这个反比例函数的解析式为
(2012•工业园区一模)如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D为x轴上动点,若CD=3AB,四边形ABCD的面积为4,则这个反比例函数的解析式为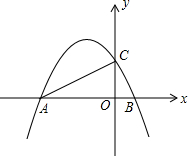 (2012•工业园区一模)如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为( )
(2012•工业园区一模)如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为( )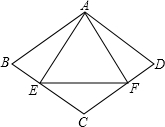 (2012•工业园区一模)如图,等腰△AEF的腰长与菱形ABCD的边长相等,其底边上的点E、F分别在BC、CD上,若∠EAF=63°,则∠B=
(2012•工业园区一模)如图,等腰△AEF的腰长与菱形ABCD的边长相等,其底边上的点E、F分别在BC、CD上,若∠EAF=63°,则∠B=