题目内容
【题目】如图，在△ABC中，∠ABC=45°，点F是高AD和BE的交点，∠CAD=30°，CD=4，求线段BF的长．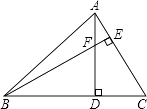 
【答案】解：∵AD⊥BC，BE⊥AC， ∴∠BEA=∠ADC=∠ADB=90°，
∴∠C+∠CBE=90°，∠C+∠CAD=90°，
∴∠DBF=∠CAD，
∵∠ABC=45°，
∴△ABD是等腰直角三角形，
∴AD=BD，
∵在△BFD和△ACD中，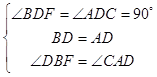 
，
∴△BFD≌△ACD（ASA），
∴BF=AC，
∵∠CAD=30°，∠ADC=90°，
∴BF=AC=2CD=8
【解析】由∠BDF=∠ADC=90°，∠DBF=∠CAD，∠DAB=∠DBA，推出BD=AD，根据ASA证△BFD≌△ACD，证出BF=AC，再由直角三角形的性质即可得出答案．
练习册系列答案
阅读快车系列答案
相关题目
