题目内容
【题目】如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.
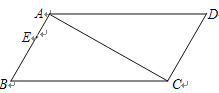
(1)求证四边形ABCD是平行四边形;
(2)当△BEP为等腰三角形时,求![]() 的值;
的值;
(3)当t=4时,把△ABP沿直线AP翻折,得到△AFP,求△AFP与□ABCD 重叠部分的面积.
【答案】(1)证明见解析(2)![]() =-237(3)
=-237(3)![]()
【解析】试题分析:(1)根据已知条件证得AB∥CD和 AD∥BC,即可判定四边形ABCD是平行四边形;(2)分点P在BC上时和当点P在AD上两种情况求解;(3)设PF与AD交于点M,则△MAP为等腰三角形 , 作MN⊥AP于N,AH⊥BP点H,可得△MPN∽△APH,再根据相似三角形的性质求解即可.
试题解析:
(1)证明:∵∠BAC=∠ACD=90°,
∴AB∥CD,
∵∠B=∠D=60°,∠BAC=∠ACD=90°,
∴∠BCA=∠CAD=30°,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)当点P在BC上时:△BEP为等边三角形,t=2,
∴![]() =-58
=-58
当点P在AD上时:EB=EP,作PH⊥AB,PA=15-t
在Rt△EHP中,由勾股定理得:![]()
∴![]() =-237
=-237
(3)设PF与AD交于点M,则△MAP为等腰三角形
作MN⊥AP于N,AH⊥BP点H,
∴△MPN∽△APH,∴![]()
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目