题目内容
【题目】如图,直线AB、CD相交于点O,OM⊥AB.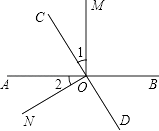
(1)若∠1=∠2,求∠NOD.
(2)若∠1= ![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
【答案】
(1)解:∵OM⊥AB,
∴∠AOM=∠1+∠AOC=90°,
∵∠1=∠2,
∴∠NOC=∠2+∠AOC=90°,
∴∠NOD=180°﹣∠NOC=180°﹣90°=90°;
(2)解:∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∵∠1= ![]() ∠BOC,
∠BOC,
∴∠BOC=∠1+90°=3∠1,
解得∠1=45°,
∠AOC=90°﹣∠1=90°﹣45°=45°,
∠MOD=180°﹣∠1=180°﹣45°=135°.
【解析】根据垂线的定义,角的运算,掌握图形间角的关系得出答案.
【考点精析】本题主要考查了对顶角和邻补角和垂线的性质的相关知识点,需要掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目