��Ŀ����
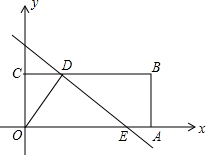 ��2013•������һģ����ͼ��ʾ���ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵĶ��㣨��˵�B��C���غϣ�������D��ֱ��y=-
��2013•������һģ����ͼ��ʾ���ı���OABC�Ǿ��Σ���A��C������ֱ�Ϊ��6��0������0��2������D���߶�BC�ϵĶ��㣨��˵�B��C���غϣ�������D��ֱ��y=-| 1 | 2 |
��1���ǡ�ODE�����ΪS����S��b�ĺ�����ϵʽ��
��2������E���߶�OA��ʱ��������OABC����ֱ��DE�ĶԳ�ͼ��Ϊ�ı���O1A1B1C1����̽���ı���O1A1B1C1�����OABC���ص����ֵ�����Ƿ����仯�������䣬������ص����ֵ���������ı䣬��˵�����ɣ�
��������1���������ֱ�߾�����A��B��Cʱ��b��ֵ��Ȼ��ֱ����ֱ��������OAB�Ľ�����OA��ʱ����2��b��3ʱ����ֱ��������OAB�Ľ�����BA��ʱ����3��b��5ʱ������⣬�������S��b�ĺ�����ϵʽ��
��2��������O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ�ı���DNEM����������ı���DNEMΪ���Σ�����tan��DEN=
��DH=2��������DNEM�ı߳�Ϊa���ɹ��ɶ���֪��a2=��4-a��2+22�������a��ֵ���̶�����ص����ֵ������
��2��������O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ�ı���DNEM����������ı���DNEMΪ���Σ�����tan��DEN=
| 1 |
| 2 |
���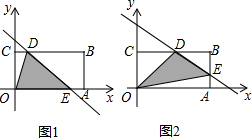 �⣺��1����ֱ�߾�����A��6��0��ʱ����b=3��
�⣺��1����ֱ�߾�����A��6��0��ʱ����b=3��
��ֱ�߾�����B��6��2��ʱ����b=5��
��ֱ�߾�����C��0��2��ʱ����b=2��
����ֱ��������OAB�Ľ�����OA��ʱ����2��b��3ʱ��
��ͼ1����ʱE��2b��0����
��S=
OE•OC=
��2b��2=2b��
����ֱ��������OAB�Ľ�����BA��ʱ����3��b��5ʱ��
��ͼ1����ʱE��6��b-3����D��2b-4��2����
��CD=2b-4��BD=6-CD=10-2b��AE=b-3��BE=AB-AE=5-b��
��S=S����OABC-S��OCD-S��DBE-S��OAE=6��2-
��2����2b-4��-
����10-2b������5-b��-
��6����b-3��=5b-b2��
��S��b�ĺ�����ϵʽΪ��S=
��
 ��2����ͼ3����O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ�ı���DNEM�������
��2����ͼ3����O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ�ı���DNEM�������
������֪��DM��NE��DN��ME��
���ı���DNEMΪƽ���ı��Σ�
������Գ�֪����MED=��NED��
�֡�MDE=��NED��
���MED=��MDE��
��MD=ME��
��ƽ���ı���DNEMΪ���Σ�
����D��DH��OA������ΪH��
������֪��tan��DEN=
��DH=2��
��HE=4��
������DNEM�ı߳�Ϊa���ɹ��ɶ���֪��a2=��4-a��2+22��
��a=
��
��S�ı���DNEM=NE•DH=5��
���ı���O1A1B1C1�����OABC���ص����ֵ����ʼ��Ϊ5��
 �⣺��1����ֱ�߾�����A��6��0��ʱ����b=3��
�⣺��1����ֱ�߾�����A��6��0��ʱ����b=3����ֱ�߾�����B��6��2��ʱ����b=5��
��ֱ�߾�����C��0��2��ʱ����b=2��
����ֱ��������OAB�Ľ�����OA��ʱ����2��b��3ʱ��
��ͼ1����ʱE��2b��0����
��S=
| 1 |
| 2 |
| 1 |
| 2 |
����ֱ��������OAB�Ľ�����BA��ʱ����3��b��5ʱ��
��ͼ1����ʱE��6��b-3����D��2b-4��2����
��CD=2b-4��BD=6-CD=10-2b��AE=b-3��BE=AB-AE=5-b��
��S=S����OABC-S��OCD-S��DBE-S��OAE=6��2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��S��b�ĺ�����ϵʽΪ��S=
|
 ��2����ͼ3����O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ�ı���DNEM�������
��2����ͼ3����O1A1��CB�ཻ�ڵ�M��OA��C1B1�ཻ�ڵ�N�������O1A1B1C1�����OABC���ص����ֵ������Ϊ�ı���DNEM�������������֪��DM��NE��DN��ME��
���ı���DNEMΪƽ���ı��Σ�
������Գ�֪����MED=��NED��
�֡�MDE=��NED��
���MED=��MDE��
��MD=ME��
��ƽ���ı���DNEMΪ���Σ�
����D��DH��OA������ΪH��
������֪��tan��DEN=
| 1 |
| 2 |
��HE=4��
������DNEM�ı߳�Ϊa���ɹ��ɶ���֪��a2=��4-a��2+22��
��a=
| 5 |
| 2 |
��S�ı���DNEM=NE•DH=5��
���ı���O1A1B1C1�����OABC���ص����ֵ����ʼ��Ϊ5��
��������������һ�κ������ۺ��⣬�����˴���ϵ������һ�κ����Ľ���ʽ�����õ��ж������ʡ������ε�����Լ����ɶ�����֪ʶ�������ѶȽϴ�ע�����ո����ߵ�������ע�����ν�ϡ���������˼���뷽��˼���Ӧ�ã�

��ϰ��ϵ�д�
 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
�����Ŀ