题目内容

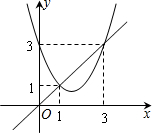函数y=x2+bx+c与y=x的图象如图，有以下结论：
①b2-4c＜0；②c-b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b-1）x+c＜0．
其中正确结论的个数为（　　）
A、1B、2C、3D、4
练习册系列答案
相关题目
方程x2+3x-1=0由于x≠0，因此可化为x+3=
1
x
，则原方程的根可视为函数y=x+3与y=
1
x
图象交点的横坐标，利用图象估计一元三次方程x3+2x2-2=0的根x0所在的范围是（　　）
A、1＜x0＜2
B、0＜x0＜l
C、-l＜x0＜0
D、-2＜x0＜-l
当x＜0时，下列函数中，函数值y为一定随自变量x的增大而增大的是（　　）
A、y=-2x+1
B、y=x2+2x-1
C、y=-
2
x
D、y=（x-1）2
已知抛物线y=ax2+bx+c（a≠0）经过点（1，1）和（-1，0）．下列结论：
①a-b+c=0；
②b2＞4ac；
③当a＜0时，抛物线与x轴必有一个交点在点（1，0）的右侧；
④抛物线的对称轴为x=-
1
4a
．
其中结论正确的个数有（　　）
A、4个B、3个C、2个D、1个
如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图，有下列5个结论：
①abc＞0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＜m （am+b）（m≠1的实数）．
其中正确结论的有（　　）
A、①②③B、①③④C、③④⑤D、②③⑤
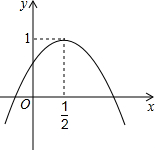如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（
1
2
，1），下列结论：①ac＜0；②a+b=0；③a=4c-4；④方程ax2+bx+c-2=0无实数根．其中正确的个数是（　　）
A、4B、3C、2D、1
已知二次函数y=ax2+2的图象开口向下，则直线y=2-ax不经过的象限是（　　）
A、第一象限B、第二象限C、第三象限D、第四象限
已知点A（a-2b，2-4ab）在抛物线y=x2+4x+10上，则点A关于抛物线对称轴的对称点坐标为（　　）
A、（-3，7）B、（-1，7）C、（-4，10）D、（0，10）
已知0≤x≤
1
2
，那么函数y=-2x2+8x-6的最大值是（　　）
A、-10.5B、2
C、-2.5D、-6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网