题目内容
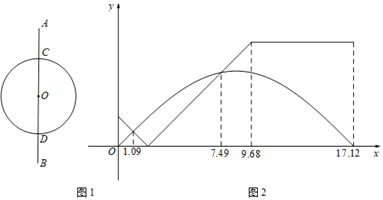
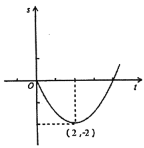
【题目】某商场开业后经历了从亏损到盈利的过程,图像刻画了该店开业以来累计利润![]() (万元)与开业时间
(万元)与开业时间![]() (月)之间的关系(累计利润是指前
(月)之间的关系(累计利润是指前![]() 个月利润总和).
个月利润总和).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)截止到第几个月,累计利润可达16万元?
(3)求第9个月的利润.
【答案】(1)S=![]() t2﹣2t;(2)截止到第8个月公司累积利润可达30万元;(3)第9个月的利润是6.5万元.
t2﹣2t;(2)截止到第8个月公司累积利润可达30万元;(3)第9个月的利润是6.5万元.
【解析】
(1)本题是通过构建函数模型解答销售利润的问题,应根据图象以及题目中所给的信息来列出S与t之间的函数关系式;
(2)把S=30代入累计利润S=![]() t2﹣2t的函数关系式里,求得月份;
t2﹣2t的函数关系式里,求得月份;
(3)分别把t=9,t=8,代入函数解析S=![]() t2﹣2t,再把总利润相减就可得出.
t2﹣2t,再把总利润相减就可得出.
解(1)设其函数关系式为:S=a(t﹣2)2﹣2.
∵所求函数关系式的图象过(0,0),
代入得:
a(0﹣2)2﹣2=0,
解得a=![]() ,
,
∴所求函数关系式为:S=![]() (t﹣2)2﹣2,即S=
(t﹣2)2﹣2,即S=![]() t2﹣2t.
t2﹣2t.
答:累积利润S与时间t之间的函数关系式为:S=![]() t2﹣2t;
t2﹣2t;
(2)把S=16代入S=![]() (t﹣2)2﹣2,
(t﹣2)2﹣2,
得 ![]() (t﹣2)2﹣2=16.
(t﹣2)2﹣2=16.
解得t1=8,t2=﹣4(舍去).
答:截止到第8个月公司累积利润可达30万元.
(3)把t=9代入关系式,
得S=![]() ×92﹣2×9=22.5,
×92﹣2×9=22.5,
由(2)可知t=8时,累计利润16万元
22.5﹣16=6.5,
答:第9个月的利润是6.5万元.

 备战中考寒假系列答案
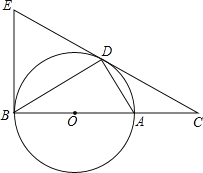
备战中考寒假系列答案【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=12,且BC=CE时,求BD的长.
【题目】根据学习函数的经验,探究函数y=x2+ax﹣4|x+b|+4(b<0)的图象和性质:
(1)下表给出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
(2)用你喜欢的方式在坐标系中画出函数y=x2+ax﹣4|x+b|+4的图象;
(3)结合你所画的函数图象,写出该函数的一条性质;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3个不同的实数解,请直接写出m的取值范围.