题目内容
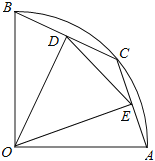
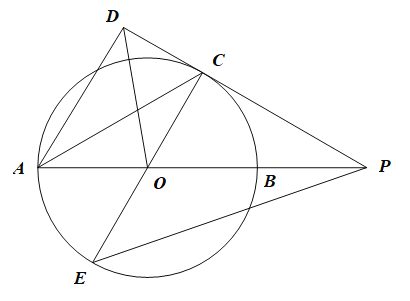
【题目】如图,![]() 、
、![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 于
于![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
(1)求证:AC是![]() 的角平分线;
的角平分线;
(2)求证:![]() ;
;
(3)若![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)详见解析;(2)详见解析;(3)2.
【解析】
(1)由PD切⊙O于点C,AD与过点C的切线垂直,易证得OC∥AD,继而证得AC平分∠DAB;
(2)根据三角形外角的性质结合直径所对的圆周角可证得![]() ,即可证得
,即可证得![]() ,从而证得结论;
,从而证得结论;
(3)设⊙O半径为R,在![]() 中,利用勾股定理结合已知
中,利用勾股定理结合已知![]() ,求得
,求得![]() ,在
,在![]() 中,求得
中,求得![]() ,得到
,得到![]() 2
2![]() ,由OC∥AD,根据平行线分线段成比例即可求得答案.
,由OC∥AD,根据平行线分线段成比例即可求得答案.
(1)∵PD切⊙O于点C,
∴OC⊥PD,
又∵AD⊥PD,
∴OC∥AD,
∴∠ACO=∠DAC.
∵OC=OA,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB;
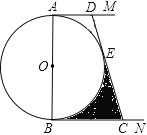
(2)连接BC,如图:
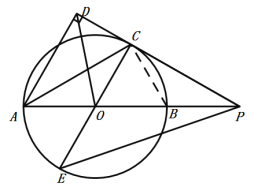
∵AB为⊙O的直径,
∴∠ACB=90![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
又![]() 是公共角,
是公共角,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)设⊙O半径为R,
在![]() 中,∠
中,∠![]() =90
=90![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() 2
2![]() ,
,![]() 3
3![]() ,
,
∴OC∥AD,
∴![]()
∴![]()
∴![]()
∴⊙![]() 的半径为
的半径为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如今很多初中生喜欢购头饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A.白开水,B.瓶装矿泉水,C.碳酸饮料,D.非碳酸饮料.根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题
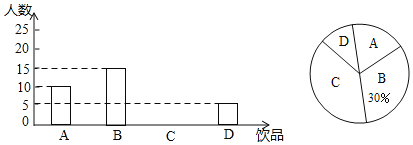
(1)这个班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如下表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名班委干部(其中有两位班长记为A,B,其余三位记为C,D,E)中随机抽取2名班委干部作良好习惯监督员,请用列表法或画树状图的方法求出恰好抽到2名班长的概率.