题目内容
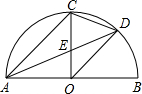 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连接CD、OD,给出以下5个结论:①OD∥AC;②AC=2CD;③CE=OE;④S△AEC=2S△DEO;⑤线段OD是DE与DA的比例中项;其中正确结论的序号是
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连接CD、OD,给出以下5个结论:①OD∥AC;②AC=2CD;③CE=OE;④S△AEC=2S△DEO;⑤线段OD是DE与DA的比例中项;其中正确结论的序号是①④
①④
.分析:①根据等腰三角形的性质和角平分线的性质,利用等量代换求证∠CAD=∠ADO即可;
②过点O作OG⊥AC,再根据直角三角形斜边大于直角边可证;
③在△AEC和△AEO中,只有∠CAD=∠DAO,其它两角都不相等,不能证明△AEC和△AEO全等,
④利用相似三角形的判定与性质以及等腰直角三角形的性质得出即可;
⑤△ADO和△DOE不相似,故线段OD不是DE与DA的比例中项.
②过点O作OG⊥AC,再根据直角三角形斜边大于直角边可证;
③在△AEC和△AEO中,只有∠CAD=∠DAO,其它两角都不相等,不能证明△AEC和△AEO全等,
④利用相似三角形的判定与性质以及等腰直角三角形的性质得出即可;
⑤△ADO和△DOE不相似,故线段OD不是DE与DA的比例中项.
解答:证明:①∵AB是半圆直径,
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=
∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∴故①选项正确.
②过点O作OG⊥AC,
∵OG⊥AC,
∴
=
,
∵半径OC⊥AB于点O,
∴
=
=
,
∴AG=GC=CD,
∴AC<2CD,
∴故②选项错误.
③∵在△AEC和△AEO中,只有∠CAD=∠DAO,其它两角都不相等,
∴不能证明△AEC和△AEO全等,
∴故③选项错误;
④过点E作EM⊥AC于点M,
∵AO=CO,AO⊥CO,
∴∠CAO=∠ACO=45°,
∴CM=ME,
∵AD平分∠CAB分别交OC于点E,
EO⊥AO,EM⊥AC,
∴ME=EO,
∴CM=ME=EO,
∴CE=
ME=
EO,
 由①得:∵AC∥OD,
由①得:∵AC∥OD,
∴△ACE∽△DOE,
∴
=
,
∴
=(
)2=2,
∴S△AEC=2S△DEO;故此选项正确,
.⑤∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAC=
×45°=22.5°,
∴∠COD=45°,
∵AC∥DO,
∴∠CAD=∠ADO=22.5°,
∴△ADO是等腰三角形,
△DOE中,∠ADO=22.5°,∠EOD=45°,
∴△ADO和△DOE不相似,
∴线段OD不是DE与DA的比例中项,
∴故⑤错误.
综上所述,只有①④正确.
故答案为:①④.
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=
| 1 |
| 2 |
∴∠CAD=∠ADO,
∴AC∥OD,
∴故①选项正确.

②过点O作OG⊥AC,
∵OG⊥AC,
∴
 |
| AG |
 |
| CG |
∵半径OC⊥AB于点O,
∴
 |
| AG |
 |
| CG |
 |
| CD |
∴AG=GC=CD,
∴AC<2CD,
∴故②选项错误.
③∵在△AEC和△AEO中,只有∠CAD=∠DAO,其它两角都不相等,
∴不能证明△AEC和△AEO全等,
∴故③选项错误;
④过点E作EM⊥AC于点M,
∵AO=CO,AO⊥CO,
∴∠CAO=∠ACO=45°,
∴CM=ME,
∵AD平分∠CAB分别交OC于点E,
EO⊥AO,EM⊥AC,
∴ME=EO,
∴CM=ME=EO,
∴CE=
| 2 |
| 2 |
 由①得:∵AC∥OD,
由①得:∵AC∥OD,∴△ACE∽△DOE,
∴
| EC |
| EO |
| 2 |
∴
| S△AEC |
| S△DEO |
| 2 |
∴S△AEC=2S△DEO;故此选项正确,
.⑤∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAC=
| 1 |
| 2 |
∴∠COD=45°,
∵AC∥DO,
∴∠CAD=∠ADO=22.5°,
∴△ADO是等腰三角形,
△DOE中,∠ADO=22.5°,∠EOD=45°,
∴△ADO和△DOE不相似,
∴线段OD不是DE与DA的比例中项,
∴故⑤错误.
综上所述,只有①④正确.
故答案为:①④.
点评:此题主要考查相似三角形的判定与性质,圆心角、弧、弦的关系,圆周角定理,等腰三角形的性质,三角形内角和定理等知识点的灵活运用,此题步骤繁琐,但相对而言,难易程度适中,很适合学生的训练是一道典型的题目.

练习册系列答案
相关题目
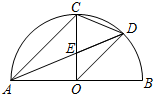 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连接CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④2CD2=CE•AB.其中正确结论的序号是
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连接CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④2CD2=CE•AB.其中正确结论的序号是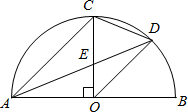 (2013•启东市一模)如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交
(2013•启东市一模)如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交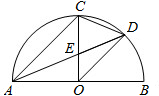 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连接CD、OD,给出以下四个结论:①AC∥OD;②CD=DE;③△ODE∽△ADO;④2CD2=CE•AB.其中正确结论的个数是( )
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连接CD、OD,给出以下四个结论:①AC∥OD;②CD=DE;③△ODE∽△ADO;④2CD2=CE•AB.其中正确结论的个数是( )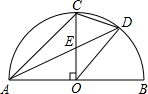 (2011•武汉模拟)如图,AB是半圆直径,半径OC⊥AB于点D,AD平分∠CAB交弧
(2011•武汉模拟)如图,AB是半圆直径,半径OC⊥AB于点D,AD平分∠CAB交弧 (2012•上城区二模)如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,交OC于点E,连接CD,OD.给出以下四个结论:①S△DEC=
(2012•上城区二模)如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,交OC于点E,连接CD,OD.给出以下四个结论:①S△DEC=