题目内容
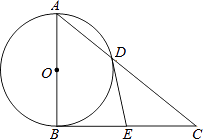
【题目】如图，某无人机于空中A处探测到目标B，D，从无人机A上看目标B，D的俯角分别为30°，60°，此时无人机的飞行高度AC为60m，随后无人机从A处继续飞行30 
m到达A′处，
（1）求A，B之间的距离；
（2）求从无人机A′上看目标D的俯角的正切值． 
【答案】
（1）解：由题意得：∠ABD=30°，∠ADC=60°，
在Rt△ABC中，AC=60m，
∴AB= 
=120（m）；
（2）过A′作A′E⊥BC交BC的延长线于E，连接A′D，
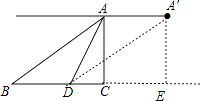
则A′E=AC=60，CE=AA′=30 
，
在Rt△ABC中，AC=60m，∠ADC=60°，
∴DC= 
AC=20 ，
∴DE=50 ，
∴tan∠AA′D=tan∠A′DC= 
= 
= 
．
答：从无人机A′上看目标D的俯角的正切值是 ．
【解析】（1）解直角三角形即可得到结论；（2）过A′作A′E⊥BC交BC的延长线于E，连接A′D，于是得到A′E=AC=60，CE=AA′=30 ，在Rt△ABC中，求得DC= AC=20 ，然后根据三角函数的定义即可得到结论．
【考点精析】掌握关于仰角俯角问题是解答本题的根本，需要知道仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
【题目】某中学数学活动小组为了调查居民的用水情况，从某社区的1500户家庭中随机抽取了30户家庭的月用水量，结果如下表所示：
月用水量（吨） | 3 | 4 | 5 | 7 | 8 | 9 | 10 |
户 数 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
（1）求这30户家庭月用水量的平均数，众数和中位数；
（2）根据上述数据，试估计该社区的月用水量；
（3）由于我国水资源缺乏，许多城市常利用分段计费的办法引导人们节约用水，即规定每个家庭的月基本用水量为m（吨），家庭月用水量不超过m（吨）的部分按原价收费，超过m吨部分加倍收费，你认为上述问题中的平均数、众数、中位数中哪一个量作为月基本用水量比较合理？简述理由。
