Question

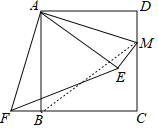
【题目】如图，在正方形ABCD中，AB＝5，点M在CD的边上，且DM＝2，△AEM与△ADM关于AM所在的直线对称，将△ADM按顺时针方向绕点A旋转90°得到△ABF，连接EF，则线段EF的长为（　　）

A.B.C.D.

Answer 1

【答案】A

【解析】

连接BM．先判定△FAE≌△MAB（SAS），即可得到EF＝BM．再根据BC＝CD＝AB＝5，CM＝3，利用勾股定理即可得到，Rt△BCM中，BM＝，进而得出EF的长．

解：如图，连接BM．

∵△AEM与△ADM关于AM所在的直线对称，

∴AE＝AD，∠MAD＝∠MAE．

∵△ADM按照顺时针方向绕点A旋转90°得到△ABF，

∴AF＝AM，∠FAB＝∠MAD．

∴∠FAB＝∠MAE

∴∠FAB+∠BAE＝∠BAE+∠MAE．

∴∠FAE＝∠MAB．

∴△FAE≌△MAB（SAS）．

∴EF＝BM．

∵四边形ABCD是正方形，

∴BC＝CD＝AB＝5．

∵DM＝2，

∴CM＝3．

∴在Rt△BCM中，BM＝，

∴EF＝，

故选：A．