题目内容
【题目】下表给出了代数式x2+bx+c与x的一些对应值:
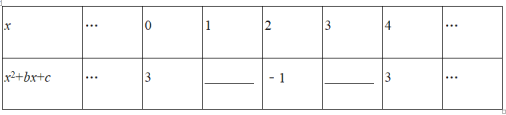
(1)请在表内的空格中填入适当的数;
(2)设y=x2+bx+c,则当x取何值时,y<0;
(3)请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象?
【答案】(1)0,0;(2)1<x<3时,y<0;(3)见解析.
【解析】
(1)把(0,3)、(2,-1)代入代数式x2+bx+c为3可求出c 与b,当x=1与x=3代入求出y即可;
(2)根据抛物线的性质得抛物线开口向上,然后找出x轴下方的抛物线所对应的自变量的范围即可;
(3)根据表中数据得到抛物线y=x2+bx+c的顶点坐标为(2,-1),然后利用点的平移规律确定抛物线的平移.
解:(1)根据题意得![]() ,
,
解得![]() ,
,
当x=1时,x2+bx+c=x2﹣4x+3=1﹣4+3=0;
当x=3时,x2+bx+c=x2﹣4x+3=9﹣12+3=0,
故答案为0,0;
(2)因为抛物线y=x2﹣4x+3的开口向上,当1<x<3时,y<0;
(3)抛物线y=x2+bx+c的顶点坐标为(2,﹣1),把点(2,﹣1)向左平移2个单位,再向上平移1个单位得到点的坐标为(0,0),
所以函数y=x2+bx+c的图象向左平移2个单位,再向上平移1个单位得到函数y=x2的图象.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目