题目内容
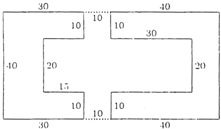 如图,是一座建筑物的平面图,其中的庭院有两处供出入的门,过路的人可以在门外观看但不能进入庭院,图中标明了该建筑物的尺寸(单位:米),所有的壁角都是直角,那么过路人看不到的门内庭院部分的面积是
如图,是一座建筑物的平面图,其中的庭院有两处供出入的门,过路的人可以在门外观看但不能进入庭院,图中标明了该建筑物的尺寸(单位:米),所有的壁角都是直角,那么过路人看不到的门内庭院部分的面积是
- A.250
- B.300
- C.400
- D.325
D
分析:首先根据过路的人可以在门外观看但不能进入庭院,找出过路人看不到的门内庭院部分的部分,再利用三角形的相似性质,求出关键点的长度,从而解决问题.
解答: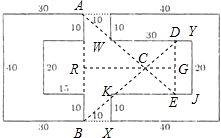 解:如图1:连接BK,并延长到D,连接AW,并延长到E,连接AB,DE,做CG⊥DE,CR⊥AB,
解:如图1:连接BK,并延长到D,连接AW,并延长到E,连接AB,DE,做CG⊥DE,CR⊥AB,
根据图上所标数据可知:
∵AB=40,DE=20,BX=KX=10,
∴KE=DE=20,
∴RG=30,
∴AB:DE=RC:CG,
CR=20,CG=10,
∴S△CED= ×20×10=100,
×20×10=100,
∴矩形EJYD面积为:20×10=200,
如图2:∵∠EAB=∠EBA=45°,
∵AB=40,
∴AE=BE=20 ,
,
∴在Rt△AEF中,EF=20,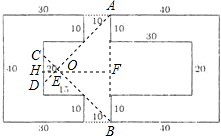
∴HE=10+15=20=5,
∵△CDE∽△BAE,
∴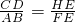 ,
,
即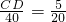 ,
,
∴CD=10,
∴S△COD= CD•HE=
CD•HE= ×10×5=25,
×10×5=25,
∴过路人看不到的门内庭院部分的面积是:200+100+25=325.
故选D.
点评:此题主要考查了相似三角形的性质以及视角与盲点问题,关键是发现盲区,从而求出它的面积,这是中考中新题型,应注意挖掘问题的本质,从而找到解决问题的办法.
分析:首先根据过路的人可以在门外观看但不能进入庭院,找出过路人看不到的门内庭院部分的部分,再利用三角形的相似性质,求出关键点的长度,从而解决问题.
解答:
 解:如图1:连接BK,并延长到D,连接AW,并延长到E,连接AB,DE,做CG⊥DE,CR⊥AB,
解:如图1:连接BK,并延长到D,连接AW,并延长到E,连接AB,DE,做CG⊥DE,CR⊥AB,根据图上所标数据可知:
∵AB=40,DE=20,BX=KX=10,
∴KE=DE=20,
∴RG=30,
∴AB:DE=RC:CG,
CR=20,CG=10,
∴S△CED=
 ×20×10=100,
×20×10=100,∴矩形EJYD面积为:20×10=200,
如图2:∵∠EAB=∠EBA=45°,
∵AB=40,
∴AE=BE=20
 ,
,∴在Rt△AEF中,EF=20,

∴HE=10+15=20=5,
∵△CDE∽△BAE,
∴
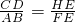 ,
,即
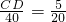 ,
,∴CD=10,
∴S△COD=
 CD•HE=
CD•HE= ×10×5=25,
×10×5=25,∴过路人看不到的门内庭院部分的面积是:200+100+25=325.
故选D.
点评:此题主要考查了相似三角形的性质以及视角与盲点问题,关键是发现盲区,从而求出它的面积,这是中考中新题型,应注意挖掘问题的本质,从而找到解决问题的办法.

练习册系列答案
相关题目
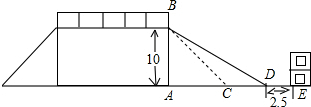 原坡脚10米的建筑物是否需要拆除?请说明理由.(参考数据:
原坡脚10米的建筑物是否需要拆除?请说明理由.(参考数据: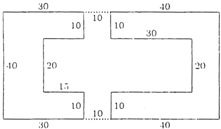 如图,是一座建筑物的平面图,其中的庭院有两处供出入的门,过路的人可以在门外观看但不能进入庭院,图中标明了该建筑物的尺寸(单位:米),所有的壁角都是直角,那么过路人看不到的门内庭院部分的面积是( )
如图,是一座建筑物的平面图,其中的庭院有两处供出入的门,过路的人可以在门外观看但不能进入庭院,图中标明了该建筑物的尺寸(单位:米),所有的壁角都是直角,那么过路人看不到的门内庭院部分的面积是( )
 ≈1.414,
≈1.414,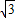 ≈1.732)
≈1.732)