题目内容
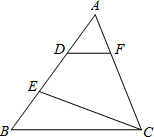
以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),则折痕EF的长为

过E作EG⊥OC,根据点B的坐标可求出OA=BC=3,OC=AB=9,设OF=x,在Rt△AOF中利用勾股定理可求出OF的长,进而可求出CF的长,同理在Rt△AEB′中利用勾股定理可求出AE的长,进而可求出BE的长,由CF-BE可得出FG的长,在Rt△EFG中利用勾股定理即可求出EF的长.
解:过E作EG⊥OC,

∵点B的坐标为(9,3),
∴OA=BC=3,OC=AB=9,设OF=x,则AF=9-x,
在Rt△AOF中,AF2=OA2+OF2,即(9-x)2=32+x2,解得x=4,
∴CF=9-4=5,
同理,设B′E=x,则AE=9-x,在Rt△AEB′中,
AE2=AB′2+B′E2,即(9-x)2=32+x2,解得x=x,即BE=4,
∴GF=CF-BE=5-4=1,
在Rt△EFG中,EF2=EG2+FG2,即EF2=32+12,EF= .
.
故答案为: .
.
解:过E作EG⊥OC,

∵点B的坐标为(9,3),
∴OA=BC=3,OC=AB=9,设OF=x,则AF=9-x,
在Rt△AOF中,AF2=OA2+OF2,即(9-x)2=32+x2,解得x=4,
∴CF=9-4=5,
同理,设B′E=x,则AE=9-x,在Rt△AEB′中,
AE2=AB′2+B′E2,即(9-x)2=32+x2,解得x=x,即BE=4,
∴GF=CF-BE=5-4=1,
在Rt△EFG中,EF2=EG2+FG2,即EF2=32+12,EF=
 .
.故答案为:
 .
.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 中,
中, 、
、 两点在
两点在 轴的上方,点
轴的上方,点 的坐标是(-1,0).以点
的坐标是(-1,0).以点 ,并把
,并把 的横坐标是2,求点
的横坐标是2,求点

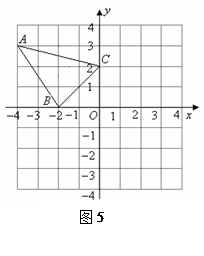
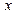 轴对称的△A1B1C1;
轴对称的△A1B1C1; 分别与x、y轴交于A
分别与x、y轴交于A  、B两点,过点B的直线交x轴负半轴于C,且
、B两点,过点B的直线交x轴负半轴于C,且 ;
; (
( )交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得
)交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由?
的值;若不存在,说明理由?