题目内容
【题目】如图所示，1925年数学家莫伦发现的世界上第一个完美长方形，它恰能被分割成10个大小不同的正方形，其中标注1、2的正方形边长分别为x、y，请你计算：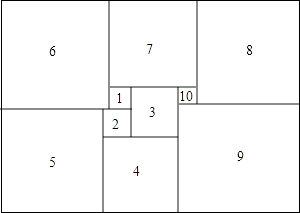 
（1）第3个正方形的边长=；第5个正方形的边长=；第10个正方形的边长= ． （用含x、y的代数式表示）
（2）当x=2时，第9个正方形的面积= ．
（3）当x、y均为正整数时，求这个完美长方形的最小周长．
【答案】
（1）x+y；x+3y；3y﹣3x
（2）100
（3）解：假设正方形1的边长为x，正方形2的边长为y，正方形3的边长为x+y，正方形4的边长为x+2y，正方形5的边长为x+3y，正方形6的边长x+3y+（y﹣x）=4y，正方形7的边长为4y﹣x，正方形8的边长为4y﹣x+3y﹣3x=7y﹣4x，正方形9的边长为10y﹣7x，正方形10的边长为4y﹣x﹣x﹣x﹣y=3y﹣3x，完美长方形存在如下关系 x+3y+4y=7y﹣4x+10y﹣7x 即可得出y=1.2x
完美长方形周长=2（x+3y+4y+x+2y+x+3y+10y﹣7x）=2（22y﹣4x）=44.8x
由于xy均为正整数，所以x=5，y=6，此时完美长方形的周长为44.8x=44.8×5=224．
答：这个完美长方形的最小周长为224
【解析】解：（1）第1、2的正方形边长分别为x、y，则第3个正方形的边长=x+y；第4个正方形的边长=x+y+y=x+2y；第5个正方形的边长=x+2y+y=x+3y；第6正方形的边长=x+3y+y﹣x=4y；第7正方形的边长=4y﹣x；第10正方形的边长=4y﹣x﹣﹣x（x+y）=3y﹣3x；
所以答案是：x+y，x+3y，3y﹣3x．（2）第9正方形的边长=x+y+x+2y﹣（3y﹣3x）=5x，
当x=2时，第9正方形的边长=5x=10，
所以第9正方形的面积为100；
所以答案是：100（3）假设正方形1的边长为x，正方形2的边长为y，正方形3的边长为x+y，正方形4的边长为x+2y，正方形5的边长为x+3y，正方形6的边长x+3y+（y﹣x）=4y，正方形7的边长为4y﹣x，正方形8的边长为4y﹣x+3y﹣3x=7y﹣4x，正方形9的边长为10y﹣7x，正方形10的边长为4y﹣x﹣x﹣x﹣y=3y﹣3x，完美长方形存在如下关系 x+3y+4y=7y﹣4x+10y﹣7x 即可得出y=1.2x
完美长方形周长=2（x+3y+4y+x+2y+x+3y+10y﹣7x）=2（22y﹣4x）=44.8x
由于xy均为正整数，所以x=5，y=6，此时完美长方形的周长为44.8x=44.8×5=224．
答：这个完美长方形的最小周长为224
【考点精析】解答此题的关键在于理解代数式求值的相关知识，掌握求代数式的值，一般是先将代数式化简，然后再将字母的取值代入；求代数式的值，有时求不出其字母的值，需要利用技巧，“整体”代入．
【题目】由于雾霾天气频发，市场上防护口罩出现热销，某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只，且所有产品当月全部售出，原料成本、销售单价及工人生产提成如表：
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
（1）若该公司五月份的销售收入为300万元，求甲、乙两种型号的产品分别是多少万只？
（2）公司实行计件工资制，即工人每生产一只口罩获得一定金额的提成，如果公司六月份投入总成本（原料总成本+生产提成总额）不超过239万元，应怎样安排甲、乙两种型号的产量，可使该月公司所获利润最大？并求出最大利润（利润=销售收入﹣投入总成本）
