Question

【题目】如图，已知抛物线y=ax2﹣5ax+2（a≠0）与y轴交于点C，与x轴交于点A（1，0）和点B．

（1）求抛物线的解析式；

（2）求直线BC的解析式；

（3）若点N是抛物线上的动点，且点N在第四象限内，过点N作NH⊥x轴，垂足为H，以B，N，H为顶点的三角形是否能够与△OBC相似？若能，请求出所有符合条件点N的坐标；若不能，请说明理由．

Answer 1

【答案】（1）y=x2﹣5ax+2；（2）y=﹣x+2；（3）（2，-1）

【解析】

试题分析：（1）把点A（1，0）在抛物线y=ax2﹣5ax+2上，解方程即可得到结论；

（2）把x=0代入y=x2﹣5ax+2，求得C（0，2），根据抛物线的对称轴为直线x=，得到B（4，0），求出直线BC的解析式y=﹣x+2；

（3）设N（x， x2﹣x+2），根据相似三角形的性质得到，即可得到结论．

试题解析：（1）∵点A（1，0）在抛物线y=ax2﹣5ax+2上，

∴a﹣5a+2=0，∴a=，

∴抛物线的解析式为：y=x2﹣5ax+2；

（2）把x=0代入y=x2﹣5ax+2，

解得：y=2，

∴C（0，2），

∵抛物线的对称轴为直线x=，

∴B（4，0），

设直线BC的解析式为：y=kx+b，

∴，

解得：k=﹣，b=2，

∴直线BC的解析式为：y=﹣x+2；

（3）设N（x， x2﹣x+2），

当△OBC∽△HBN时，如图，

∴，

即，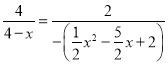

解得：x1=2，x2=4（不合题意舍去）

故N的坐标为（2，-1）