题目内容
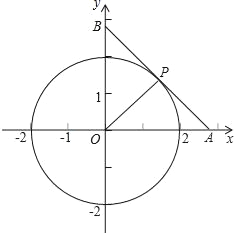
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.
(1)求证:△OBP与△OPA相似;
(2)当点P为AB中点时,求出P点坐标;
(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.
【答案】(1)见解析;(2)P点坐标是(![]() ,
, ![]() );(3)存在;Q点坐标是(
);(3)存在;Q点坐标是(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)在Rt△OAB中,由切线的性质知:OP⊥AB,易证得△OAP∽△BPO.
(2)当P为AB中点时,由于OP⊥AB,那么OP平分∠AOB,即P点的横、纵坐标相等,已知OP的长,易求得点P的坐标.
(3)此题应分两种情况:
①OP为对角线,此时OQ∥AP,由于∠OPA=90°,那么∠POQ=90°,即△POQ是等腰直角三角形,已知OA⊥OB,那么OB⊥PQ,此时OB为∠POQ的对角线,即P、Q关于y轴对称由此得解;
②OP为边,此时OP∥AQ,由于∠OPA=90°,那么平行四边形OPAQ为矩形,即∠POQ是等腰直角三角形,解法同①.
解:(1)证明:
∵AB是过点P的切线,
∴AB⊥OP,∴∠OPB=∠OPA=90°;
∴在Rt△OPB中,∠1+∠3=90°,
又∵∠BOA=90°∴∠1+∠2=90°,
∴∠2=∠3;
在△OPB中△APO中,
∴△OPB∽△APO.
(2)∵OP⊥AB,且PA=PB,
∴OA=OB,
∴△AOB是等腰三角形,
∴OP是∠AOB的平分线,
∴点P到x、y轴的距离相等;
又∵点P在第一象限,
∴设点P(x,x)(x>0),
∵圆的半径为2,
∴OP=![]() ,解得x=
,解得x=![]() 或x=﹣
或x=﹣![]() (舍去),
(舍去),
∴P点坐标是(![]() ,
,![]() ).
).
(3)存在;
①如图设OAPQ为平行四边形,∴PQ∥OA,OQ∥PA;
∵AB⊥OP,∴OQ⊥OP,PQ⊥OB,
∴∠POQ=90°,
∵OP=OQ,
∴△POQ是等腰直角三角形,
∴OB是∠POQ的平分线且是边PQ上的中垂线,
∴∠BOQ=∠BOP=45°,
∴∠AOP=45°,
设P(x,x)、Q(﹣x,x)(x>0),
∵OP=2代入得![]() ,解得x=
,解得x=![]() ,
,
∴Q点坐标是(﹣![]() ,
,![]() );(1分)
);(1分)
②如图示OPAQ为平行四边形,
同理可得Q点坐标是(![]() ,﹣
,﹣![]() ).
).




【题目】某校为了解全校学生上学期参加“生涯规划”社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | b | m |
15<x≤18 | 2 | n |
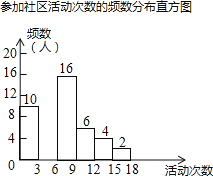
根据以上图表信息,解答下列问题:
(1)表中a= , b= , m= , n= .
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);