题目内容
 光线以如图所示的角度α照射到平面镜Ⅰ上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=60°,∠β=50°,∠γ为度.
光线以如图所示的角度α照射到平面镜Ⅰ上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=60°,∠β=50°,∠γ为度.
- A.40°
- B.50°
- C.60°
- D.70°
A
分析:利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角和角之间的相互转换来求解.
解答:如答图所示,过A作MA⊥AC,垂足为A,
则∠1=90°-α=90°-60°=30°,
∴∠2=∠1=30°,
∴∠7=90°-30°=60°,
过B作BN⊥m,垂足为B,
∴∠3=90°-β=90°-50°=40°,
∴∠ABC=∠3+∠4=2∠3=2×40°=80°,
过C作CE⊥AC,垂足为C,
则∠5=∠6,∠BCD=2∠5+Y=∠7+∠ABC=60°+80°=140°,
∵∠5+Y=90°,
∴∠6=∠5=50°,
∴∠Y=90°-50°=40°.
故选:A.
点评:此题考查了镜面反射的原理与性质.需注意利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角,利用平行的性质把相应的角转移到一个三角形中求解.
分析:利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角和角之间的相互转换来求解.
解答:如答图所示,过A作MA⊥AC,垂足为A,
则∠1=90°-α=90°-60°=30°,
∴∠2=∠1=30°,

∴∠7=90°-30°=60°,
过B作BN⊥m,垂足为B,
∴∠3=90°-β=90°-50°=40°,
∴∠ABC=∠3+∠4=2∠3=2×40°=80°,
过C作CE⊥AC,垂足为C,
则∠5=∠6,∠BCD=2∠5+Y=∠7+∠ABC=60°+80°=140°,
∵∠5+Y=90°,
∴∠6=∠5=50°,
∴∠Y=90°-50°=40°.
故选:A.
点评:此题考查了镜面反射的原理与性质.需注意利用反射的性质得到入射光线与水平线的夹角等于反射光线与水平线的夹角,利用平行的性质把相应的角转移到一个三角形中求解.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
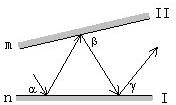
 9、光线以如图所示的角度α,照射到平面镜I上,然后在平面镜I、II之间来回反射,已知∠α=50°,∠β=60°,则∠γ等于( )
9、光线以如图所示的角度α,照射到平面镜I上,然后在平面镜I、II之间来回反射,已知∠α=50°,∠β=60°,则∠γ等于( )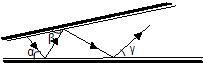
 6、光线以如图所示的角度a照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射.已知∠α=60°,∠β=50°,求∠γ.
6、光线以如图所示的角度a照射到平面镜I上,然后在平面镜I、Ⅱ之间来回反射.已知∠α=60°,∠β=50°,求∠γ.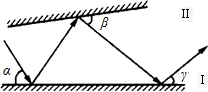 光线以如图所示的角度α照射到平面镜Ⅰ上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=60°,∠β=50°,∠γ为( )度.
光线以如图所示的角度α照射到平面镜Ⅰ上,然后在平面镜Ⅰ、Ⅱ之间来回反射,已知∠α=60°,∠β=50°,∠γ为( )度.