题目内容
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压 p(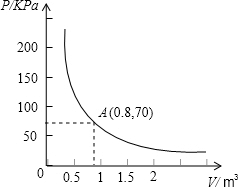 kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
kPa)是气体体积V(m3)的反比例函数,其图象如图所示. (1)写出这一函数的表达式;
(2)当气压100p(kPa)时,气体体积是多少?
(3)当气球内的气压大于140p(kPa)时,气球将爆炸.为了安全起见,气体的体积应不小于多少?
分析:(1)设函数解析式为P=
,把点(0.8,70)的坐标代入函数解析式求出k值,即可求出函数关系式;
(2)将P=100代入(1)中的函数式中,可求气球的体积V.
(3)依题意P≤140,即 56V≤140,解不等式即可.
| K |
| V |
(2)将P=100代入(1)中的函数式中,可求气球的体积V.
(3)依题意P≤140,即 56V≤140,解不等式即可.
解答:解:(1)设P与V的函数关系式为P=
,
则 k=0.8×70,
解得k=56,
∴函数关系式为P=
.
(2)将P=100代入P=
中,
得
=100,
解得V=0.56,
∴当气球内的气压为10kPa时,气球的体积为0.56立方米.
(3)当P>140KPa时,气球将爆炸,
∴P≤140,即
≤140,
解得 V≥0.4(m3).
故为了安全起见,气体的体积应不小于0.4(m3).
| K |
| V |
则 k=0.8×70,
解得k=56,
∴函数关系式为P=
| 56 |
| V |
(2)将P=100代入P=
| 56 |
| V |
得
| 56 |
| V |
解得V=0.56,
∴当气球内的气压为10kPa时,气球的体积为0.56立方米.
(3)当P>140KPa时,气球将爆炸,
∴P≤140,即
| 56 |
| V |
解得 V≥0.4(m3).
故为了安全起见,气体的体积应不小于0.4(m3).
点评:本题考查了反比例函数的实际应用,关键是建立函数关系式,并会运用函数关系式解答题目的问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
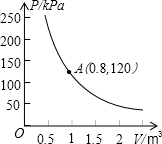 某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kpa)与气体体积v(m3)成反比例函数,其图象如图所示,当气球内的气压大于140kpa时,气球将会爆炸,为了安全起见,请你求出气体体积的范围.
某气球内充满了一定质量的气体,当温度不变时,气球内的气压p(kpa)与气体体积v(m3)成反比例函数,其图象如图所示,当气球内的气压大于140kpa时,气球将会爆炸,为了安全起见,请你求出气体体积的范围.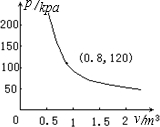
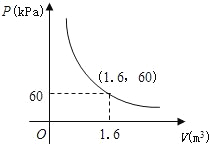 体体积V(m3)的反比例函数,其图象如图所示.
体体积V(m3)的反比例函数,其图象如图所示. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )