题目内容
菱形ABCD的两条对角线交于点O.且A0,B0的长分别为方程x2-7x+12=0的两个根,则这个菱形的边长为
- A.5
- B.4
- C.3
- D.6
A
分析:把已知方程左边利用十字相乘法分解因式,然后根据两数之积为0,这两个因式至少有一个为0,转化为两个一元一次方程,求出方程的解得到原方程的解,可得出OA及OB的长,又四边形ABCD为菱形,根据菱形的对角线互相垂直得到三角形AOB为直角三角形,根据勾股定理求出AB的长,即为菱形的边长.
解答:x2-7x+12=0,
分解因式得:(x-3)(x-4)=0,
可得:x-3=0或x-4=0,
解得:x1=3,x2=4,
∴OA=3,OB=4或OA=4,OB=3,
又ABCD为菱形,
∴AC⊥BD,即△AOB为直角三角形,
根据勾股定理得:AB=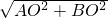 =5,
=5,
则这个菱形的边长为5.
故选A.
点评:此题考查了利用因式分解法解一元二次方程,以及菱形的性质,利用因式分解法求一元二次方程的解的步骤为:将方程右边化为0,方程左边分解为两个一次因式的乘积,然后根据两数相乘积为0,得到两因式至少有一个为0,转化为两个一元一次方程来求解.
分析:把已知方程左边利用十字相乘法分解因式,然后根据两数之积为0,这两个因式至少有一个为0,转化为两个一元一次方程,求出方程的解得到原方程的解,可得出OA及OB的长,又四边形ABCD为菱形,根据菱形的对角线互相垂直得到三角形AOB为直角三角形,根据勾股定理求出AB的长,即为菱形的边长.
解答:x2-7x+12=0,
分解因式得:(x-3)(x-4)=0,
可得:x-3=0或x-4=0,
解得:x1=3,x2=4,
∴OA=3,OB=4或OA=4,OB=3,
又ABCD为菱形,
∴AC⊥BD,即△AOB为直角三角形,
根据勾股定理得:AB=
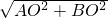 =5,
=5,则这个菱形的边长为5.
故选A.
点评:此题考查了利用因式分解法解一元二次方程,以及菱形的性质,利用因式分解法求一元二次方程的解的步骤为:将方程右边化为0,方程左边分解为两个一次因式的乘积,然后根据两数相乘积为0,得到两因式至少有一个为0,转化为两个一元一次方程来求解.

练习册系列答案
相关题目

 )。
)。 )。
)。