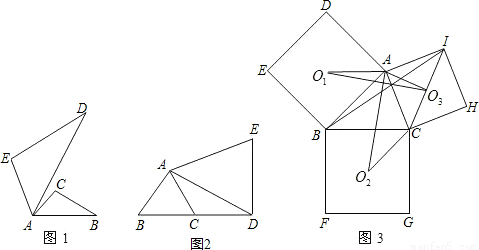
题目内容
一个三角形三个内角度数的比是2:3:4,这个三角形是 三角形.
- A.锐角
- B.直角
- C.钝角
- D.等边
A
分析:已知三角形三个内角的度数之比,可以设一份为k,根据三角形的内角和等于180°列方程求三个内角的度数,从而确定三角形的形状.
解答:三个内角的度数分别为2k,3k,4k.
则2k+3k+4k=180°,
解得k=20°,
∴2k=40°,3k=60°,4k=80°,
∴这个三角形是锐角三角形.
故选A.
点评:本题主要考查了内角和定理.解答此类题利用三角形内角和定理列方程求解可简化计算.
分析:已知三角形三个内角的度数之比,可以设一份为k,根据三角形的内角和等于180°列方程求三个内角的度数,从而确定三角形的形状.
解答:三个内角的度数分别为2k,3k,4k.
则2k+3k+4k=180°,
解得k=20°,
∴2k=40°,3k=60°,4k=80°,
∴这个三角形是锐角三角形.
故选A.
点评:本题主要考查了内角和定理.解答此类题利用三角形内角和定理列方程求解可简化计算.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点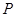 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 以点
以点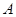 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 的长为
的长为  ;
; 的三边
的三边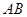 ,
,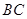 ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 的长为
的长为  ;
; 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
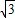 ,90°),得到△ADE,则线段BD的长为______cm;
,90°),得到△ADE,则线段BD的长为______cm;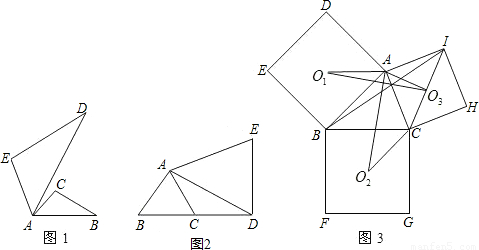
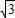 ,90°),得到△ADE,则线段BD的长为______cm;
,90°),得到△ADE,则线段BD的长为______cm;