题目内容
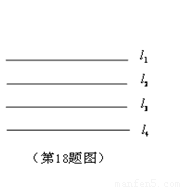
如图，平面内4条直线l1、l2、l3、l4是一组平行线，相邻2条平行线的距离都是1个单位长度，正方形ABCD的4个顶点A、B、C、D都在这些平行线上，其中点A、C分别在直线l1、l4上，该正方形的面积是分析：因为A、C分别在直线l1、l4上，那么B，D也应该在直线l1、l4上，一种情况是正方形的边和平行先垂直的时候，一种是按照“弦图”画出时，分别求出边长，从而求出面积．
解答：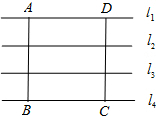
解：（1）当正方形的边长和平行线垂直时，
正方的边长应该为3，所以正方的面积为：3×3=9．
（2）如图，将两条平行的虚线之间分为三段，使每一段长为1个单位，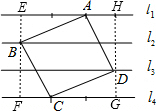
由题意可知：△AEB≌△AHD≌BFC≌CGD，
所以当正方形如图放置时，正方形的边长为：
=
．
所以正方形的面积为：
×
=5．
故答案为9或5．
解：（1）当正方形的边长和平行线垂直时，正方的边长应该为3，所以正方的面积为：3×3=9．
（2）如图，将两条平行的虚线之间分为三段，使每一段长为1个单位，
由题意可知：△AEB≌△AHD≌BFC≌CGD，
所以当正方形如图放置时，正方形的边长为：
| 22+12 |
| 5 |
所以正方形的面积为：
| 5 |
| 5 |
故答案为9或5．
点评：本题考查正方形的性质，正方形的边长相等，四个角都是直角，以及勾股定理的运用，关键是知道分不同的情况进行求解．
练习册系列答案
相关题目
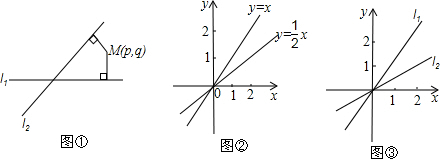
3、如图，平面内三条直线交于点O，∠1=30°，∠2=60°，AB与CD的关系是（ ）