题目内容
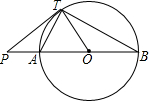 已知:如图PT是⊙O的切线,T为切点,PAB是经过圆心O的割线.
已知:如图PT是⊙O的切线,T为切点,PAB是经过圆心O的割线.(1)求证:∠PTA=∠BTO;
(2)若PT=4,PA=2,求sinB的值.
分析:(1)根据切线性质和圆周角定理得出∠PTO=∠ATB,都减去∠ATO即可;
(2)求出AB,求出TM,根据勾股定理求出BT,解直角三角形求出即可.
(2)求出AB,求出TM,根据勾股定理求出BT,解直角三角形求出即可.
解答:(1)证明:∵PT是⊙O的切线,
∴∠PTO=90°,
∵AB是⊙O直径,
∴∠ATB=90°,
∴∠PTO-∠ATO=∠ATB-∠ATO,
∴∠PTA=∠BTO.
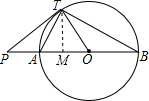 (2)解:过点T作TM⊥AB于点M,
(2)解:过点T作TM⊥AB于点M,
∵OT=OB,
∴∠B=∠BTO,
∵由(1)知:∠PTA=∠BTO,
∴∠PTA=∠B,
∵∠P=∠P,
∴△PTA∽△PBT,
∴
=
,
∵PT=4,PA=2,
∴PB=8,
∴AB=8-2=6,OT=3,
在△PTO中,由三角形面积公式得:
PT•OT=
PO•TM,
∴4×3=(2+3)•TM,
∴TM=
=2.4,
在Rt△TMO中,由勾股定理得:OM=
=1.8,
即BM=3+1.8=4.8,
在Rt△TMB中,由勾股定理得:BT=
=
,
∴sinB=
=
=
.
∴∠PTO=90°,
∵AB是⊙O直径,
∴∠ATB=90°,
∴∠PTO-∠ATO=∠ATB-∠ATO,
∴∠PTA=∠BTO.
 (2)解:过点T作TM⊥AB于点M,
(2)解:过点T作TM⊥AB于点M,∵OT=OB,
∴∠B=∠BTO,
∵由(1)知:∠PTA=∠BTO,
∴∠PTA=∠B,
∵∠P=∠P,
∴△PTA∽△PBT,
∴
| PT |
| PA |
| PB |
| PT |
∵PT=4,PA=2,
∴PB=8,
∴AB=8-2=6,OT=3,
在△PTO中,由三角形面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
∴4×3=(2+3)•TM,
∴TM=
| 12 |
| 5 |
在Rt△TMO中,由勾股定理得:OM=
| 32-2.42 |
即BM=3+1.8=4.8,
在Rt△TMB中,由勾股定理得:BT=
| 32+4.82 |
| ||
| 5 |
∴sinB=
| TM |
| BT |
| 2.4 | ||||
|
| ||
| 267 |
点评:本题考查了解直角三角形,相似三角形的性质和判定,勾股定理,三角形面积,切线的性质的应用,主要考查学生的推理能力和计算能力.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
 点作⊙O的割线PAB(PB>PA).设PA=x,PB=y.
点作⊙O的割线PAB(PB>PA).设PA=x,PB=y.
 S△PBT?若存在,请求出PA的值;若不存在,请说明理由.
S△PBT?若存在,请求出PA的值;若不存在,请说明理由.
 S△PBT?若存在,请求出PA的值;若不存在,请说明理由.
S△PBT?若存在,请求出PA的值;若不存在,请说明理由.