题目内容
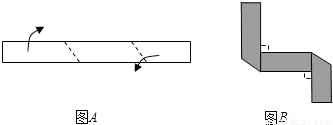
将长为20cm，宽为2cm的矩形白色纸条，折成如图所示的图形，并在其一面着色，则着色部分的面积为 ．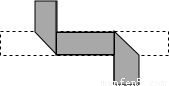
【答案】分析：根据折叠的性质，已知图形的折叠就是已知两个图形全等．由图知，着色部分的面积是原来的纸条面积减去两个等腰直角三角形的面积．
解答：解：着色部分的面积=原来的纸条面积-两个等腰直角三角形的面积=20×2-2×
×2×2=36cm2．
故答案为：36cm2．
点评：本题考查图形的折叠变化及等腰直角三角形的面积公式，解题关键是要理解折叠是一种对称变换，难度一般．
解答：解：着色部分的面积=原来的纸条面积-两个等腰直角三角形的面积=20×2-2×
×2×2=36cm2．故答案为：36cm2．
点评：本题考查图形的折叠变化及等腰直角三角形的面积公式，解题关键是要理解折叠是一种对称变换，难度一般．
练习册系列答案
阅读快车系列答案
相关题目
如图A所示，将长为20cm，宽为2cm的长方形白纸条，折成图B所示的图形并在其一面着色，则着色部分的面积为（ ）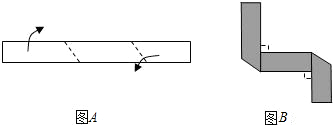
| A、34cm2 | B、36cm2 | C、38cm2 | D、40cm2 |
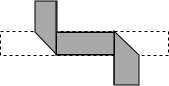将长为20cm，宽为2cm的矩形白色纸条，折成如图所示的图形，并在其一面着色，则着色部分的面积为
