题目内容
已知抛物线 (a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数
(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数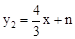 的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
 (a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数
(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数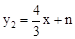 的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.x<-2
解:∵OC=8,且点C在y轴上,
∴一次函数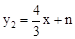 中 n=为8或-8 。
中 n=为8或-8 。
①当n=8时,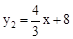 ,如图1,
,如图1,
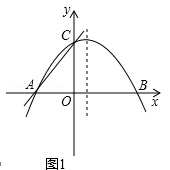
令 ,得x=-6。
,得x=-6。
∴A(-6,0)。
∵抛物线经过点A、C,且与x轴交点A、B在原点的两侧,
∴抛物线开口向下,则a<0。
∵AB=16,且A(-6,0),∴B(10,0)。
∵A、B关于对称轴对称,∴对称轴直线x=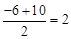 。
。
要使y1随着x的增大而减小,则x>2。
②当n=-8时, ,如图2,
,如图2,

令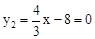 ,得x=6。∴A(6,0)。
,得x=6。∴A(6,0)。
∵抛物线经过点A、C,且与x轴交点A、B在原点的两侧,
∴抛物线开口向下,则a>0。
∵AB=16,且A(6,0),∴B(-10,0)。
∵A、B关于对称轴对称,∴对称轴直线x= 。
。
要使y1随着x的增大而减小,则x<-2。
综上所述,当n=8,y1随着x的增大而减小时,自变量x的取值范围为x>2;当n=-8,y1随着x的增大而减小时,自变量x的取值范围为x<-2。
根据OC的长度确定出n的值为8或﹣8,然后分n=8和n=﹣8两种情况求出点A的坐标,确定抛物线开口方向并求出点B的坐标,再求出抛物线的对称轴解析式,然后根据二次函数的增减性求出x的取值范围。
∴一次函数
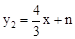 中 n=为8或-8 。
中 n=为8或-8 。①当n=8时,
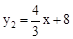 ,如图1,
,如图1,
令
 ,得x=-6。
,得x=-6。∴A(-6,0)。
∵抛物线经过点A、C,且与x轴交点A、B在原点的两侧,
∴抛物线开口向下,则a<0。
∵AB=16,且A(-6,0),∴B(10,0)。
∵A、B关于对称轴对称,∴对称轴直线x=
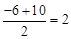 。
。要使y1随着x的增大而减小,则x>2。
②当n=-8时,
 ,如图2,
,如图2,
令
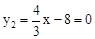 ,得x=6。∴A(6,0)。
,得x=6。∴A(6,0)。∵抛物线经过点A、C,且与x轴交点A、B在原点的两侧,
∴抛物线开口向下,则a>0。
∵AB=16,且A(6,0),∴B(-10,0)。
∵A、B关于对称轴对称,∴对称轴直线x=
 。
。要使y1随着x的增大而减小,则x<-2。
综上所述,当n=8,y1随着x的增大而减小时,自变量x的取值范围为x>2;当n=-8,y1随着x的增大而减小时,自变量x的取值范围为x<-2。
根据OC的长度确定出n的值为8或﹣8,然后分n=8和n=﹣8两种情况求出点A的坐标,确定抛物线开口方向并求出点B的坐标,再求出抛物线的对称轴解析式,然后根据二次函数的增减性求出x的取值范围。

练习册系列答案
相关题目
 的对称轴是直线x=2.
的对称轴是直线x=2.
 的值是否发生变化?若发生变化,说明理由;若不发生变化,求出
的值是否发生变化?若发生变化,说明理由;若不发生变化,求出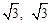 ),对称轴为直线
),对称轴为直线 ,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=
,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=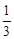 MP,MD=
MP,MD=
 。
。 上,请用含k的代数式表示b;
上,请用含k的代数式表示b;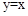 上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,B3,…,Bn,以线段AnBn为边向右作正方形AnBnCnDn,若这组抛物线中有一条经过点Dn,求所有满足条件的正方形边长。
 的长;
的长;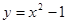 的顶点坐标是( )
的顶点坐标是( )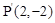 ,点A的对应点为
,点A的对应点为 ,则抛物线上PA段扫过的区域(阴影部分)的面积为 .
,则抛物线上PA段扫过的区域(阴影部分)的面积为 .
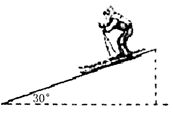
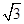 米
米 的自变量x的取值范围是 .
的自变量x的取值范围是 .