题目内容
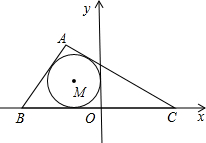 如图,△ABC的内切圆的圆心是M(-1,1),B(
如图,△ABC的内切圆的圆心是M(-1,1),B(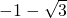 ,0),C(
,0),C(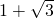 ,0),则△ABC的面积S的值是________.
,0),则△ABC的面积S的值是________.
3+2
分析:连接BE,则BE过M,根据三角形的内切圆求出BE过M,根据点的坐标求出∠CBE=30°,根据线段的垂直平分线性质求出∠ACB=∠EBC=30°,求出∠A=90°,根据直角三角形性质和勾股定理求出AC和AB,根据三角形的面积求出即可.
解答: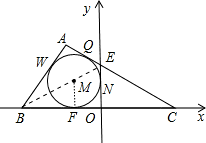 解:连接BE,
解:连接BE,
∵圆M切AC于E,切BC于F,切AB于W,切Y轴于N,
∴BW=BF,EQ=EN,
则BE过M,
∵M(-1,1),B(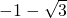 ,0),C(
,0),C(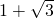 ,0),
,0),
∴BF=1+ -1=
-1= ,MF=1,
,MF=1,
由勾股定理得:BM=2,
∴MF= BM,
BM,
∴∠EBC=30°,
∴∠ABC=60°,
∵X轴⊥Y轴,
∵OC=OB=1+ ,
,
∴EB=EC,
∴∠ACB=∠ABC=30°,
∴∠A=180°-∠B-∠C=90°,
∴AB= BC=
BC= ×(2+2
×(2+2 )=1+
)=1+ ,
,
由勾股定理得:AC=3+ ,
,
∴三角形ABC的面积是 AC×AB=
AC×AB= ×(1+
×(1+ )×(3+
)×(3+ )=3+2
)=3+2 .
.
故答案为:3+2 .
.
点评:本题主要考查对勾股定理,线段的垂直平分线性质,三角形的面积,三角形的内角和定理,含30度角的直角三角形的性质,三角形的内切圆与内心,坐标与图形性质等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

分析:连接BE,则BE过M,根据三角形的内切圆求出BE过M,根据点的坐标求出∠CBE=30°,根据线段的垂直平分线性质求出∠ACB=∠EBC=30°,求出∠A=90°,根据直角三角形性质和勾股定理求出AC和AB,根据三角形的面积求出即可.
解答:
 解:连接BE,
解:连接BE,∵圆M切AC于E,切BC于F,切AB于W,切Y轴于N,
∴BW=BF,EQ=EN,
则BE过M,
∵M(-1,1),B(
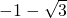 ,0),C(
,0),C(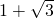 ,0),
,0),∴BF=1+
 -1=
-1= ,MF=1,
,MF=1,由勾股定理得:BM=2,
∴MF=
 BM,
BM,∴∠EBC=30°,
∴∠ABC=60°,
∵X轴⊥Y轴,
∵OC=OB=1+
 ,
,∴EB=EC,
∴∠ACB=∠ABC=30°,
∴∠A=180°-∠B-∠C=90°,
∴AB=
 BC=
BC= ×(2+2
×(2+2 )=1+
)=1+ ,
,由勾股定理得:AC=3+
 ,
,∴三角形ABC的面积是
 AC×AB=
AC×AB= ×(1+
×(1+ )×(3+
)×(3+ )=3+2
)=3+2 .
.故答案为:3+2
 .
.点评:本题主要考查对勾股定理,线段的垂直平分线性质,三角形的面积,三角形的内角和定理,含30度角的直角三角形的性质,三角形的内切圆与内心,坐标与图形性质等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
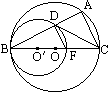
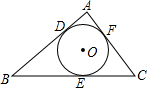 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
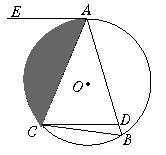
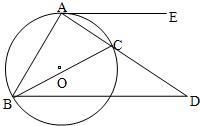 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.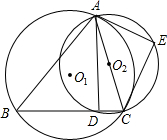 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3