题目内容
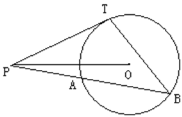
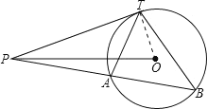
【题目】已知:如图,点P是半径为5cm的⊙O外的一点,OP= 13cm,PT切⊙O于T点,过点P作PB(PB>PA),设PA= x,PB= y。
(1)求y与x的函数解析式,并确定自变量x的取值范围;
(2)这个函数有最大值吗?若有求出此时△PBT的面积,若没有,请说明理由;
(3)是否存在这样的PB,使得![]() ,若存在,请求出PA的值,若不存在,请说明理由.
,若存在,请求出PA的值,若不存在,请说明理由.
【答案】(1)y=![]() (8<x<12);(2)有最大值,当PAB与PO重合时y最大, y最大=18, 这时
(8<x<12);(2)有最大值,当PAB与PO重合时y最大, y最大=18, 这时![]() ;
;
(3)存在这样的PB,A是PB的中点,这时,PA=x=6![]() .
.
【解析】
(1)连接圆心和切线,求得切线长,利用切割线定理可求得y关于x的函数解析式;(2)根据自变量的取值,求得函数的最值,进而求得面积;(3)利用三角形相似的面积求得相应的对应边的长.
(1)连接OT,∵PT切⊙O于T点,
∴∠OTP=90°,
∵OP=13cm,OT=5cm,
∴PT=12,
∵PT为切线,
∴PT2=PA×PB
∴xy=144,
∴y=![]() (8<x<12);
(8<x<12);
(2)由(1)得x=8时,y最大=18,此时TB为直径,TB=10,
∴S△PBT=![]()
(3)∵∠TPA=∠TPA, ∠PTA=∠PBT,
∴△PTA∽△PBT
∵![]()
∴PA:PT=1:![]()
∵PT=12,
∴PA=6![]()
∵在自变量的取值范围内,故存在.

练习册系列答案
相关题目