��Ŀ����
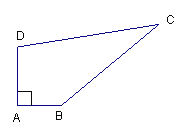
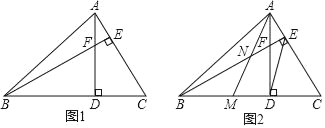
����Ŀ����ͼ1���������ABC�У���ABC=45�㣬����AD��BE�ཻ�ڵ�F��
��1���ж�BF��AC��������ϵ��˵�����ɣ�
��2����ͼ2������ACD���߶�AD���ۣ���C����BD�ϵĵ�M��AM��BE�ཻ�ڵ�N����DE��AMʱ���ж�NE��AC��������ϵ��˵�����ɣ�
���𰸡���1��BF=AC�����ɼ���������2��NE=![]() AC�����ɼ�����.
AC�����ɼ�����.
�������������������1����ͼ1��֤����ADC�ա�BDF��AAS�����ɵ�BF=AC��
��2����ͼ2�����۵��ã�MD=DC���ȸ�����������λ�ߵ����ۿɵã�AE=EC�����߶δ�ֱƽ���ߵ����ʵã�AB=BC�����ABE=��CBE����ϣ�1���ã���BDF�ա�ADM�����DBF=��MAD�����֤����ANE=��NAE=45�㣬��AE=EN������EN=![]() AC��
AC��
���������
��1��BF=AC�������ǣ�
��ͼ1����AD��BC��BE��AC��
���ADB=��AEF=90����
�ߡ�ABC=45����
���ABD�ǵ���ֱ�������Σ�
��AD=BD��
�ߡ�AFE=��BFD��
���DAC=��EBC��
����ADC����BDF��
��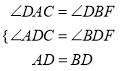 ��
��
���ADC�ա�BDF��AAS����
��BF=AC��
��2��NE=![]() AC�������ǣ�
AC�������ǣ�
��ͼ2�����۵��ã�MD=DC��
��DE��AM��
��AE=EC��
��BE��AC��
��AB=BC��
���ABE=��CBE��
�ɣ�1���ã���ADC�ա�BDF��
�ߡ�ADC�ա�ADM��
���BDF�ա�ADM��
���DBF=��MAD��
�ߡ�DBA=��BAD=45����
���DBA����DBF=��BAD����MAD��
����ABE=��BAN��
�ߡ�ANE=��ABE+��BAN=2��ABE��
��NAE=2��NAD=2��CBE��
���ANE=��NAE=45����
��AE=EN��
��EN=![]() AC��
AC��
�����͡������
��������
19
����Ŀ��ijУѧ�������������ѧ���������ѡ��һ�����µ�ѧ������ϯ���Լס��ҡ���������ѡ�˽����˱��Ժ����ԣ����˵IJ��Գɼ����±���ʾ��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 75 | 80 | 90 |
���� | 93 | 70 | 68 |
����¼�ó���ѧУ��֯200��ѧ������ͶƱ�Ƽ��ķ�ʽ�������˽����������������˵�Ʊ��������ͳ��ͼ��ʾ��û����Ȩ��ÿλͬѧֻ���Ƽ�1�ˣ���ÿ��1Ʊ��1����
��1���ֱ����������������ĵ÷֣�
��2������ʵ����Ҫ��ѧУ�����ԡ����ԡ�������������÷ְ�3��3��4�ı���ȷ�����˳ɼ���������˭�ᵱѡѧ������ϯ��
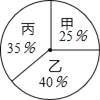
���𰸡���1���÷�50�֣��ҵ÷�80�֣����÷�70�֣���2���ҵ�ѡѧ������ϯ��
�������������������1������������Էֱ���ü��ұ����˵���������÷֣�
��2������������Էֱ���ü��ұ����˵����ճɼ���Ȼ��Ƚϴ�С���ɽ���⣮
���������(1)������ɵã�
����������ĵ÷��ǣ�200��25%=50(��)��
����������ĵ÷��ǣ�200��40%=80(��)��
����������ĵ÷��ǣ�200��35%=70(��)��
(2)������ɵã�
�ijɼ��ǣ� ![]() (��)��
(��)��
�ҵijɼ��ǣ� ![]() (��)��
(��)��
���ijɼ��ǣ� ![]() (��)��
(��)��
��70.4<73.9<77��
���ҵ�ѡѧ������ϯ��

 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�����Ŀ��Ϊ�˷ḻ�����˵���������ס�������λ����֯����ְ����ij�羰������.�ס�������λ����ְ����![]() �ˣ������ҵ�λ��������
�ˣ������ҵ�λ��������![]() �ˣ��Ҽ�λ��������
�ˣ��Ҽ�λ��������![]() ��.���˽⣬�÷羰������Ʊ�۸����±�:
��.���˽⣬�÷羰������Ʊ�۸����±�:
����(��) |
|
|
|
����(Ԫ/��) |
|
|
|
�������λ�ֱ�������Ʊ��һ��Ӧ��![]() Ԫ.
Ԫ.
��1���ס�������λ���ж���������ְ�����μ����棿
��2�������λ��![]() ������ְ��������ԭ����������棬��ô���м��ֹ�����ͨ���Ƚϣ������ι�����Ʊ������ʡǮ��
������ְ��������ԭ����������棬��ô���м��ֹ�����ͨ���Ƚϣ������ι�����Ʊ������ʡǮ��