题目内容
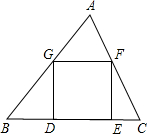如图，△ABC是锐角三角形，正方形DEFG的一边在BC上，其余两个定点在AB，AC上，记△ABC的面积为S1，正方形的面积为S2，则
- A.S1≥2S2
- B.S1≤2S2
- C.S1＞2S2
- D.S1＜2S2
A
分析：根据题意，易得△AGF∽△ABC，△BDG∽△BMA，再将△ABC的面积S1表示出来，再将正方形DEFG的面积表示出来，利用S1-2S2进行比较．
解答：
解：过点A作BC上的高AM交BC于点M，交GF于点N，
S1=
BC×AM，S2=GF×GD=GF2
∵GF∥BC，DG∥AM
∴△AGF∽△ABC，△BDG∽△BMA，
∴
=
，
=
=
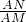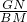，GN=DM，BD+DM=BM
∴+=+
=
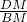=1
∴GF×（AM+BC）=AM×BC，
∴GF=
∴2×S2=2×（）2
∴S1-2S2=
-2（）2=（1-
）
=
×
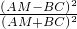≥0
∴S1≥2S2．故选A．
点评：本题综合考查相似三角形和正方形的性质．
分析：根据题意，易得△AGF∽△ABC，△BDG∽△BMA，再将△ABC的面积S1表示出来，再将正方形DEFG的面积表示出来，利用S1-2S2进行比较．
解答：
解：过点A作BC上的高AM交BC于点M，交GF于点N，S1=
BC×AM，S2=GF×GD=GF2∵GF∥BC，DG∥AM
∴△AGF∽△ABC，△BDG∽△BMA，
∴
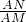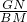=，==，GN=DM，BD+DM=BM∴
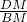+=+==1∴GF×（AM+BC）=AM×BC，
∴GF=
∴2×S2=2×（
）2∴S1-2S2=
-2（）2=（1-）=
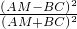×≥0∴S1≥2S2．故选A．
点评：本题综合考查相似三角形和正方形的性质．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
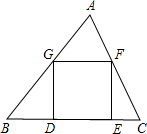如图，△ABC是锐角三角形，正方形DEFG的一边在BC上，其余两个定点在AB，AC上，记△ABC的面积为S1，正方形的面积为S2，则（ ）| A、S1≥2S2 | B、S1≤2S2 | C、S1＞2S2 | D、S1＜2S2 |
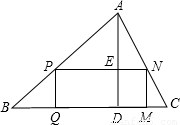
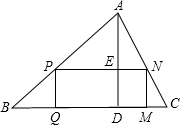如图，△ABC是锐角三角形，BC=120，高AD=80，矩形PQMN的顶点P、N分别在AB、AC上，M、Q在BC上，AD与PN交于点E，请问矩形PQMN的面积什么时候最大，最大面积是多少？
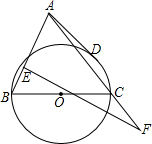如图，△ABC是锐角三角形，以BC为直径作⊙O，AD是⊙O的切线，从AB上一点E作AB的垂线交AC的延长线于F，若