Question

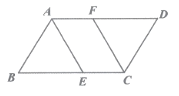
【题目】如图，在ABCD中，AB=2，BC=3，∠BAD=120°，AE平分∠BAD，交BC于点E，过点C作CF∥AE，交AD于点F，则四边形AECF的面积为________．

Answer 1

【答案】

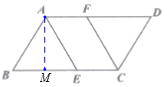
【解析】如图所示，过点A作AM⊥BC，垂足为M，先证明△ABE是等边三角形，从而求得BE=AB=2，继而求得AM长，再证明四边形AECF是平行四边形，继而根据平行四边形的面积公式进行计算即可求得.

如图所示，过点A作AM⊥BC，垂足为M，

∵四边形ABCD是平行四边形，

∴AD//BC，

∴∠B=180°-∠BAD=180°-120°=60°，

∠DAE=∠AEB，

∵AE平分∠BAD，∠BAD=120°，

∴∠DAE=60°，

∴∠AEB=60°，

∴△ABE是等边三角形，

∴BE=AB=2，

∴BM=1，AM=，

又∵CF//AE，∴四边形AECF是平行四边形，

∵CE=BC-BE=3-2=1，

∴S四边形AECF=CEAM=，

故答案为：.