Question

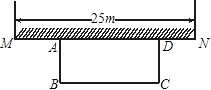
【题目】如图所示，四边形ABCD中，AD∥BC，∠A＝90°，∠BCD＜90°，AB＝7，AD＝2，BC＝3，试在边AB上确定点P的位置，使得以P、C、D为顶点的三角形是直角三角形．

Answer 1

【答案】在线段AB上且距离点A为1、6、处．

【解析】

分∠DPC＝90°，∠PDC＝90，∠PDC＝90°三种情况讨论，在边AB上确定点P的位置，根据相似三角形的性质求得AP的长，使得以P、A、D为顶点的三角形是直角三角形．

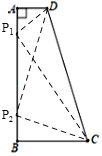
（1）如图，当∠DPC＝90°时，

∴∠DPA+∠BPC＝90°，

∵∠A＝90°，

∴∠DPA+∠PDA＝90°，

∴∠BPC＝∠PDA，

∵AD∥BC，

∴∠B=180°-∠A=90°，

∴∠A＝∠B，

∴△APD∽△BCP，

∴，

∵AB=7，BP=AB-AP，AD=2，BC=3，

∴，

∴AP2﹣7AP+6＝0，

∴AP＝1或AP＝6，

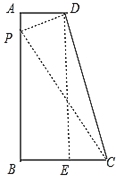
（2）如图：当∠PDC＝90°时，过D点作DE⊥BC于点E，

∵AD//BC，∠A=∠B=∠BED=90°，

∴四边形ABED是矩形，

∴DE＝AB＝7，AD=BE=2，

∵BC＝3，

∴EC＝BC-BE=1，

在Rt△DEC中，DC2＝EC2+DE2＝50，

设AP＝x，则PB＝7﹣x，

在Rt△PAD中PD2＝AD2+AP2＝4+x2，

在Rt△PBC中PC2＝BC2+PB2＝32+（7﹣x）2，

在Rt△PDC中PC2＝PD2+DC2 ，即32+（7﹣x）2＝50+4+x2，

解方程得：．

（3）当∠PDC＝90°时，

∵∠BCD＜90°，

∴点P在AB的延长线上，不合题意；

∴点P的位置有三处，能使以P、A、D为顶点的三角形是直角三角形，分别在线段AB上且距离点A为1、6、处．