题目内容
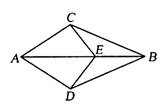
如图,AC平分∠BAD,CM⊥AB,且AB+AD=2AM,那么∠ADC与∠ABC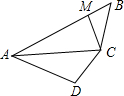
- A.相等
- B.互补
- C.和为150°
- D.和为165°
B
分析:可过点C作CN⊥AD,交AD的延长线于点N,通过作辅助线得出Rt△ACM≌Rt△ACN,Rt△BCM≌Rt△DCN,得出对应角相等,进而再通过角之间的转化,即可得出结论.
解答: 解:过点C作CN⊥AD,交AD的延长线于点N,
解:过点C作CN⊥AD,交AD的延长线于点N,
∵AC平分∠BAD,CM⊥AB,CN⊥AD,
∴CM=CN,
在Rt△ACM≌Rt△ACN中,
∵ ,
,
∴Rt△ACM≌Rt△ACN,
∴AM=AN,
又∵AB+AD=2AM,
∴BM=DN,
在Rt△BCM与Rt△DCN,
∵
∴Rt△BCM≌Rt△DCN(SAS),
∴∠ABC=∠CDN,
∴∠ADC+∠ABC=∠ADC+∠CDN=180°,
∴∠ADC与∠ABC互补.
故选B.
点评:本题主要考查了全等三角形的判定及性质问题,能够通过作辅助线熟练求解此类问题.
分析:可过点C作CN⊥AD,交AD的延长线于点N,通过作辅助线得出Rt△ACM≌Rt△ACN,Rt△BCM≌Rt△DCN,得出对应角相等,进而再通过角之间的转化,即可得出结论.
解答:
 解:过点C作CN⊥AD,交AD的延长线于点N,
解:过点C作CN⊥AD,交AD的延长线于点N,∵AC平分∠BAD,CM⊥AB,CN⊥AD,
∴CM=CN,
在Rt△ACM≌Rt△ACN中,
∵
 ,
,∴Rt△ACM≌Rt△ACN,
∴AM=AN,
又∵AB+AD=2AM,
∴BM=DN,
在Rt△BCM与Rt△DCN,
∵

∴Rt△BCM≌Rt△DCN(SAS),
∴∠ABC=∠CDN,
∴∠ADC+∠ABC=∠ADC+∠CDN=180°,
∴∠ADC与∠ABC互补.
故选B.
点评:本题主要考查了全等三角形的判定及性质问题,能够通过作辅助线熟练求解此类问题.

练习册系列答案
相关题目
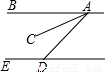
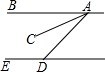 (2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是
(2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是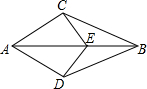 如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )