题目内容
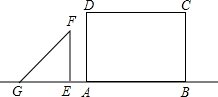 (2013•铁岭)如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是( )
(2013•铁岭)如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是( )分析:设GE=a,EF=b,AE=m,AB=c,Rt△EFG向右匀速运动的速度为1,分类讨论:当E点在点A左侧时,S=0,其图象为在x轴的线段;当点G在点A左侧,点E在点A右侧时,AE=t-m,GA=a-(t-m)=a+m-t,易证得△GAP∽△GEF,利用相似比可表示PA=
(a+m-t),S为图形PAEF的面积,则S=
[
(a+m-t)]•(t-m),可发现S是t的二次函数,且二次项系数为负数,所以抛物线开口向下;当点G在点A右侧,点E在点B左侧时,S为定值,定义三角形GEF的面积,其图象为平行于x轴的线段;当点G在点B左侧,点E在点B右侧时,和前面一样运用相似比可表示出PB=
(a+m+c-t),S为△GPB的面积,则S=
(t-a-m-c)2,则S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上.
| b |
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| a |
| b |
| 2a |
解答:解:设GE=a,EF=b,AE=m,AB=c,Rt△EFG向右匀速运动的速度为1,
当E点在点A左侧时,S=0;
当点G在点A左侧,点E在点A右侧时,如图,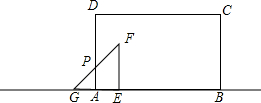
AE=t-m,GA=a-(t-m)=a+m-t,
∵PA∥EF,
∴△GAP∽△GEF,
∴
=
,即
=
∴PA=
(a+m-t),
∴S=
(PA+FE)•AE=
[
(a+m-t)]•(t-m)
∴S是t的二次函数,且二次项系数为负数,所以抛物线开口向下;
当点G在点A右侧,点E在点B左侧时,S=
ab;
当点G在点B左侧,点E在点B右侧时,如图,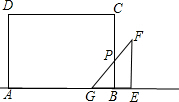
GB=a+m+c-t,
∵PA∥EF,
∴△GBP∽△GEF,
∴
=
,
∴PB=
(a+m+c-t),
∴S=
GB•PB=
(a+m+c-t)•
(a+m+c-t)=
(t-a-m-c)2,
∴S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上,
综上所述,S与t的图象分为四段,第一段为x轴上的一条线段,第二段为开口向下的抛物线的一部分,第三段为与x轴平行的线段,第四段为开口向上的抛物线的一部分.
故选D.
当E点在点A左侧时,S=0;
当点G在点A左侧,点E在点A右侧时,如图,

AE=t-m,GA=a-(t-m)=a+m-t,
∵PA∥EF,
∴△GAP∽△GEF,
∴
| PA |
| EF |
| GA |
| GE |
| PA |
| b |
| a+m-t |
| a |
∴PA=
| b |
| a |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| a |
∴S是t的二次函数,且二次项系数为负数,所以抛物线开口向下;
当点G在点A右侧,点E在点B左侧时,S=
| 1 |
| 2 |
当点G在点B左侧,点E在点B右侧时,如图,

GB=a+m+c-t,
∵PA∥EF,
∴△GBP∽△GEF,
∴
| PB |
| EF |
| GB |
| GE |
∴PB=
| b |
| a |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| a |
| b |
| 2a |
∴S是t的二次函数,且二次项系数为,正数,所以抛物线开口向上,
综上所述,S与t的图象分为四段,第一段为x轴上的一条线段,第二段为开口向下的抛物线的一部分,第三段为与x轴平行的线段,第四段为开口向上的抛物线的一部分.
故选D.
点评:本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 (2013•铁岭)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(2013•铁岭)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE. (2013•铁岭)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
(2013•铁岭)如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( ) (2013•铁岭)如图是4块小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小方块的个数,其主视图是( )
(2013•铁岭)如图是4块小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小方块的个数,其主视图是( ) (2013•铁岭)如图,点P是正比例函数y=x与反比例函数y=
(2013•铁岭)如图,点P是正比例函数y=x与反比例函数y=