Question

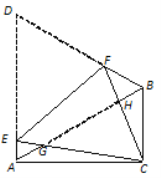
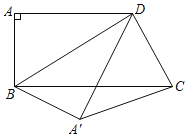
【题目】如图，在四边形ABCD中，AD∥BC，∠A＝90°，∠ADC＝120°，连接BD，把△ABD沿BD翻折，得到△A′BD，连接A′C，若AB＝3，∠ABD＝60°，则点D到直线A′C的距离为（　　）

A.B.C.D.

Answer 1

【答案】C

【解析】

过点D作DE⊥A′C于E，过A'作A'F⊥CD于F，由直角三角形的性质得出BD＝2AB＝6，AD＝AB＝3，求出∠BDC＝90°，由三角函数得出CD＝tan∠DBCBD＝2，由折叠的性质得∠A'DB＝∠ADB＝30°，A'D＝AD＝3，求出∠DA'F＝30°，由直角三角形的性质得出DF＝A'D＝，A'F＝DF＝，得出CF＝CD﹣DF＝，由勾股定理得出A'C＝，再由面积法求出DE即可．

过点D作DE⊥A′C于E，过A'作A'F⊥CD于F，如图所示：

∵AD∥BC，

∴∠ADB＝∠DBC，∠ADC+∠BCD＝180°，∠BCD＝180°﹣120°＝60°，

∵∠ABD＝60°，

∴∠ADB＝30°，

∴BD＝2AB＝6，AD＝AB＝3，∠BDC＝∠ADC﹣∠ADB＝120°﹣30°＝90°，∠DBC＝30°，

∴CD＝tan∠DBCBD＝tan30°×6＝×6＝2，

由折叠的性质得：∠A'DB＝∠ADB＝30°，A'D＝AD＝3，

∴∠A'DC＝120°﹣30°﹣30°＝60°，

∵A'F⊥CD，

∴∠DA'F＝30°，

∴DF＝A'D＝，A'F＝DF＝，

∴CF＝CD﹣DF＝2﹣＝，

∴A'C＝＝，

∵△A'CD的面积＝A'C×DE＝CD×A'F，

∴，

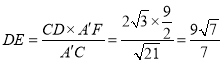即D到直线A′C的距离为；

故选：C．