题目内容
【题目】如图,已知在Rt△ABC中,∠C=900,AD是∠BAC的角分线.
(1)以AB上的一点O为圆心,AD为弦在图中作出⊙O.(不写作法,保留作图痕迹);
(2)试判断直线BC与⊙O的位置关系,并证明你的结论;

【答案】(1)作图见解析;(2)相切;证明见解析.
【解析】试题分析(1)因为AD是弦,所以圆心O即在AB上,也在AD的垂直平分线上;
(2)因为D在圆上,所以只要能证明OD⊥BC就说明BC为⊙O的切线.
试题解析:(1)如图所示,
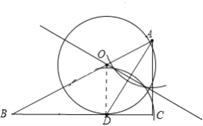
(2)相切;理由如下:
证明:连结OD,
∵OA=OD,
∴∠OAD=∠ODA
∵AD是BAC的角平分线,则∠OAD=∠DAC,
∴∠ODA=∠DAC,
∵AC⊥BC,则∠DAC+∠ADC=90°,
∴∠ODA+∠ADC=90°,即∠ODC=90°,
∴OD⊥BC,
即BC是⊙O的切线.

练习册系列答案
相关题目
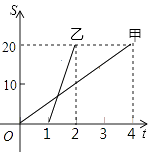
【题目】已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:
(1)结合问题情境分析: ①y与x的函数表达式为;②自变量x的取值范围是 .
(2)下表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … |
|
| 5 | 4 | m |
|
| … |
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
【题目】甲、乙、丙、丁参加体育训练,近期10次跳绳测试的平均成绩都是每分钟174个,其方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差 | 0.023 | 0.018 | 0.020 | 0.021 |
则这10次跳绳中,这四个人发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁